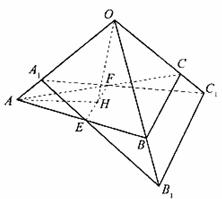
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)、求异面直线AB与MD所成角的大小;
(Ⅱ)、求平面![]() 与平面
与平面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
 |
答案
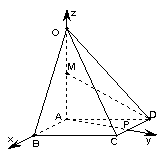
解: 作![]() 于点P,如图,分别以AB,AP,AO
于点P,如图,分别以AB,AP,AO
所在直线为![]() 轴建立坐标系,
轴建立坐标系,
则![]() ,
,
![]() …………………2分
…………………2分
(Ⅰ)设![]() 与
与![]() 所成的角为
所成的角为![]() ,
,![]() ,
,
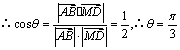 ,
, ![]()
![]() 与
与![]() 所成角的大小为
所成角的大小为![]() …5分
…5分
(Ⅱ)![]() ,
,![]() 设平面OCD的法向量为
设平面OCD的法向量为![]() ,
,
则![]() ,即
,即 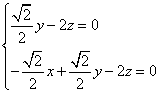 ,取
,取![]() ,解得
,解得![]() … 6分
… 6分
易知 平面OAB的一个法向量为![]() ………7分
………7分
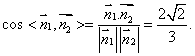 ……………………………………………………9分
……………………………………………………9分
由图形知,平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() …………………10分
…………………10分

 ;
;  的坐标为(h,k)。
的坐标为(h,k)。