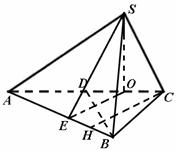
一个三棱锥![]() 的三视图、直观图如图.
的三视图、直观图如图.
(1)求三棱锥![]() 的体积;
的体积;
(2)求点C到平面SAB的距离;
(3)求二面角![]() 的余弦值.
的余弦值.
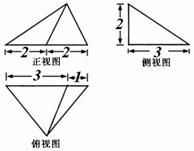
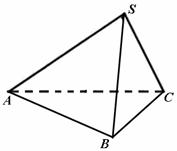
答案
解: (1)由正视图、俯视图知![]() ;
;
由正视图、侧视图知,点B在平面SAC上的正投影为AC的中点D,则![]() ,
,
![]() 平面
平面![]() ,
,![]() ;
;
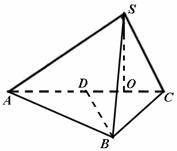 由俯视图、侧视图知,点S在平面ABC上的正投影为DC的中点O,
由俯视图、侧视图知,点S在平面ABC上的正投影为DC的中点O,
则![]() ,
,![]() 平面
平面![]() ,
,![]() .如图.
.如图.
(1)三棱锥![]() 的体积
的体积![]() .
.
解法一:
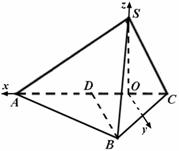 以O为原点,OA为
以O为原点,OA为![]() 轴,过O且平行于BD的直线为
轴,过O且平行于BD的直线为![]() 轴,OS为
轴,OS为![]() 轴,建立如图空间直角坐标系,可求
轴,建立如图空间直角坐标系,可求![]() ,
,![]() ,
,
设![]() 是平面SAB的一个法向量,则
是平面SAB的一个法向量,则
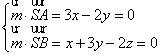 ,取
,取![]() ,
,
(2)可知![]() ,设点C到平面SAB的距离为
,设点C到平面SAB的距离为![]() ,
,
则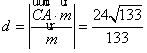 .
.
(3)可知![]() 是平面ABC一个法向量,故
是平面ABC一个法向量,故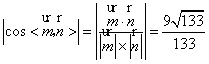 ,
,
二面角![]() 的余弦值为
的余弦值为![]() .
.
解法二:
 (2)可求
(2)可求![]() ,
,![]() ,
,
![]() ,
,
△SAB的面积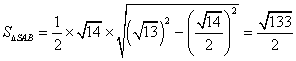 ,
,
设点C到平面SAB的距离为![]() ,
,
由三棱锥![]() 的体积
的体积![]() ,
,
得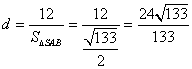 .
.
(3)作![]() 于H,作
于H,作![]() 交AB于E,则
交AB于E,则![]() ,
,
连接SE,因OE是SE在底面ABC内的射影,而![]() ,故
,故![]() ,
,
![]() 为二面角
为二面角![]() 的平面角.
的平面角.
△ABC中,易求![]() ,
,
由△ABC的面积,![]() ,
,![]() ,
,
△AEO与△AHC相似,相似比为AO:AC=3:4,故![]() ,
,
![]() 中,
中,![]() ,
,
故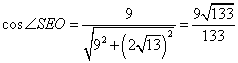 ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() .
.