设函数![]() 在R上可导,其导函数为
在R上可导,其导函数为![]() ,且函数
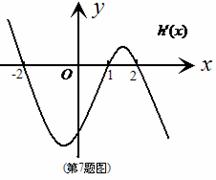
,且函数![]() 的图象如图所示,则函数
的图象如图所示,则函数![]() 有下列结论中一定成立的是
有下列结论中一定成立的是
A.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
B.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
C.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
D.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
答案
D
设函数![]() 在R上可导,其导函数为
在R上可导,其导函数为![]() ,且函数
,且函数![]() 的图象如图所示,则函数
的图象如图所示,则函数![]() 有下列结论中一定成立的是
有下列结论中一定成立的是
A.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
B.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
C.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()
D.![]() 有极大值
有极大值![]() 和极小值
和极小值![]()

D
 ,则f在[a,b]上可积,且
,则f在[a,b]上可积,且 ,这称为牛顿-莱布尼茨公式,它也常写成
,这称为牛顿-莱布尼茨公式,它也常写成 。
。 ,则f在[a,b]上可积,且
,则f在[a,b]上可积,且 ,这称为牛顿-莱布尼茨公式,它也常写成
,这称为牛顿-莱布尼茨公式,它也常写成 。
。基本定理:
若函数f(x)在[a,b]上连续,且存在原函数F(x),即 ,则f在[a,b]上可积,且
,则f在[a,b]上可积,且 ,这称为牛顿-莱布尼茨公式,它也常写成
,这称为牛顿-莱布尼茨公式,它也常写成 。
。
基本积分公式:


登录并加入会员可无限制查看知识点解析