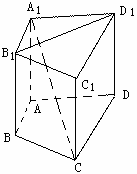
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.
(1)求异面直线A1M和C1D1所成的角的正切值;
(2)证明:平面ABM⊥平面A1B1M.

答案
方法1:(1)如图,因为C1D1∥B1A1,所以∠MA1B1为异面直线A1M与C1D1所成的角.
因为A1B1⊥平面BCC1B1,所以∠A1B1M=90°,
而A1B1=1,B1M=![]() =
=![]() ,故
,故
tan∠MA1B1=![]() =
=![]() .
.
即异面直线A1M和C1D1所成的角的正切值为![]() .
.
(2)证明:由A1B1⊥平面BCC1B1,BM⊂平面平面BCC1B1,得A1B1⊥BM①
由(1)知,B1M=![]() ,
,
又BM=![]() =
=![]() ,B1B=2,
,B1B=2,
所以B1M2+BM2=B1B2,从而BM⊥B1M②
又A1B1∩B1M=B1,∴BM⊥平面A1B1M,而BM⊂平面ABM,因此平面ABM⊥平面A1B1M.
方法2:以A为原点,![]() ,
,![]() ,
,![]() 的方向分别作为x、y、z轴的正方向,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),A1(0,0,2),B1(1,0,2),C1(1,1,2),D1(0,1,2),M(1,1,1).
的方向分别作为x、y、z轴的正方向,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),A1(0,0,2),B1(1,0,2),C1(1,1,2),D1(0,1,2),M(1,1,1).

 设异面直线A1M与C1D1所成角为α,则cosα=
设异面直线A1M与C1D1所成角为α,则cosα=![]() ,
,
∴tanα=![]() .
.
即异面直线A1M和C1D1所成的角的正切值是![]() .
.
 又B1M∩A1B1=B1,
又B1M∩A1B1=B1,
∴BM⊥平面A1B1M,而BM⊂平面ABM,
因此ABM⊥平面A1B1M.


 。
。  α∩β=l,且P∈l。
α∩β=l,且P∈l。