为检测某种零件的生产质量，检验人员需抽取同批次的零件样本进行检测并评分．若检测后评分结果大于60分的零件为合格零件，评分结果不超过40分的零件将直接被淘汰，评分结果在
内的零件可能被修复也可能被淘汰．
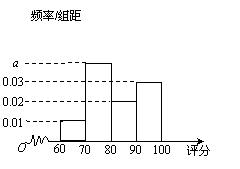
（Ⅰ）已知200个合格零件的评分结果的频率分布直方图
如图所示．请根据此频率分布直方图，估计这200
个零件评分结果的平均数和众数；
（Ⅱ）根据已有的经验，可能被修复的零件个体被修复的概率如下表：
| 零件评分结果所在区间 |
|
|
| 每个零件个体被修复的概率 |
|
|
假设每个零件被修复与否相互独立．现有5个零件的评分结果为（单位：分）：38，43，
45，52，58，记这5个零件被修复的个数为随机变量X，求X的分布列和数学期望．
答案
（Ⅰ）∵
，
∴平均数
，众数为75．
（Ⅱ）由题意可知：评分结果在
，
内零件各有2个，则随机变量X的所有可能取值为0，1，2，3，4．
，
，
，
，
，
X的分布列为：
| X | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
∴
=0.1x+10