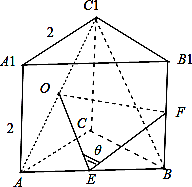
在直三棱柱ABC﹣A₁B₁C₁中，AC=AA₁=2，∠ACB=90°，点E，F分别是棱AB，BB₁的中点，当二面角C₁﹣AA₁﹣B为45°时，直线EF与BC₁的夹角为（　　）

A．60° B．45° C．90° D．120°

答案

C【考点】两直线的夹角与到角问题．

【专题】转化思想；综合法；直线与圆；空间角．

【分析】先将EF平移到AB₁，再利用中位线进行平移，使两条异面直线移到同一点，得到直线EF和BC₁所成的角，求之即可．

【解答】解：由题意可得∠CAB=45°为二面角C₁﹣AA₁﹣B的平面角，△ABC为等腰直角三角形，

连AC₁，取AC₁得中点O，∵E，F分别是棱AB，BB₁的中点，∴OE平行且等于BC₁，

∠OEF=θ或其补角，即为直线EF与BC₁的夹角．

由于OE=BC₁=，EF===，OF==，

由余弦定理可得cosθ==0，

∴θ=90°，

故选：C．

【点评】本题主要考查了异面直线及其所成的角，平移法是研究异面直线所成的角的最常用的方法，经常考查，属于中档题．