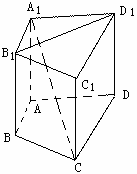
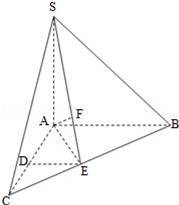
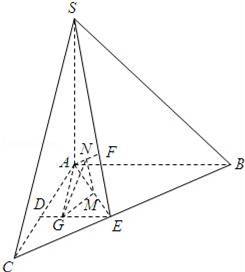
如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE.
(1)求证:AF⊥平面SBC;
(2)在线段上DE上是否存在点G,使二面角G﹣AF﹣E的大小为30°?若存在,求出DG的长;若不存在,请说明理由.

答案
【考点】二面角的平面角及求法;直线与平面垂直的判定.
【分析】(1)通过证明AF与平面SBC内的两条相交直线垂直即可;
(2)抓住两点找到问题的求解方向:一是点G的预设位置,二是二面角G﹣AF﹣E的位置,计算即可.
【解答】(1)证明:由AC=AB=SA=2,AC⊥AB,E是BC的中点,得![]()
![]() .
.
因为SA⊥底面ABC,所以SA⊥AE.
在Rt△SAE中,![]()
![]() ,所以
,所以![]()
![]() .
.
因此AE2=EF•SE,又因为∠AEF=∠AES,
所以△EFA∽△EAS,
则∠AFE=∠SAE=90°,即AF⊥SE.
因为SA⊥底面ABC,所以SA⊥BC,又BC⊥AE,
所以BC⊥底面SAE,则BC⊥AF.
又SE∩BC=E,所以AF⊥平面SBC.
(2)结论:在线段上DE上存在点G使二面角G﹣AF﹣E的大小为30°,此时DG=![]()
![]() .
.
理由如下:
假设满足条件的点G存在,并设DG=t.
过点G作GM⊥AE交AE于点M,
又由SA⊥GM,AE∩SA=A,得GM⊥平面SAE.
作MN⊥AF交AF于点N,连结NG,则AF⊥NG.
于是∠GNM为二面角G﹣AF﹣E的平面角,
即∠GNM=30°,由此可得![]()
![]() .
.
由MN∥EF,得![]()
![]() ,
,
于是有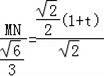
 ,
,![]()
![]() .
.
在Rt△GMN中,MG=MNtan30°,
即![]()
![]() ,解得
,解得![]()
![]() .
.
于是满足条件的点G存在,且![]()
![]() .
.



 。
。  α∩β=l,且P∈l。
α∩β=l,且P∈l。