已知2sin2α=1+cos2α,则tan(α+![]() )的值为( )
)的值为( )
A.﹣3 B.3 C.﹣3或3 D.﹣1或3
答案
D【考点】两角和与差的正切函数.
【分析】由倍角公式求得sinα与cosα的数量关系,结合正弦、余弦以及正切函数的转化关系进行解答即可.
【解答】解:∵2sin2α=1+cos2α,
∴4sinαcosα=1+2cos2α﹣1,
即2sinαcosα=cos2α,
①当cosα=0时,![]() ,此时
,此时![]() ,
,
②当cosα≠0时,![]() ,此时
,此时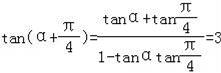 ,
,
综上所述,tan(α+![]() )的值为﹣1或3.
)的值为﹣1或3.
故选:D.
