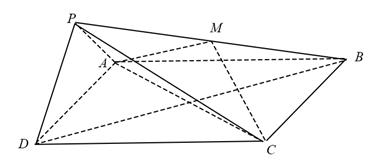
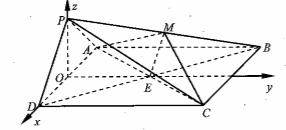
如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
答案
(Ⅰ)详见解析:(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】

试题解析:解:(I)设![]() 交点为
交点为![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点.
的中点.
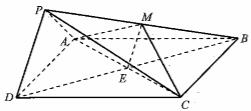
(II)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是正方形,所以
是正方形,所以![]() .
.
如图建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则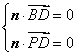 ,即
,即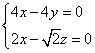 .
.
令![]() ,则
,则![]() ,
,![]() .于是
.于是![]() .
.
平面![]() 的法向量为
的法向量为![]() ,所以
,所以![]() .
.
由题知二面角![]() 为锐角,所以它的大小为
为锐角,所以它的大小为![]() .
.
(III)由题意知![]() ,
,![]() ,
,![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【考点】1.线线,线面的位置关系;2.向量法.
【名师点睛】本题涉及到了立体几何中的线面平行与垂直的判定与性质,全面考查立体几何中的证明与求解,意在考查学生的空间想象能力和逻辑推理能力;利用空间向量解决立体几何问题是一种成熟的方法,要注意建立适当的空间直角坐标系以及运算的准确性.
