已知抛物线C：y2=2px过点P（1，1）.过点（0，
）作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP，ON交于点A，B，其中O为原点.
（Ⅰ）求抛物线C的方程，并求其焦点坐标和准线方程；
（Ⅱ）求证：A为线段BM的中点.
答案
（Ⅰ）方程为
，抛物线C的焦点坐标为（
，0），准线方程为
.（Ⅱ）详见解析.
【解析】
试题分析：（Ⅰ）代入点
求得抛物线的方程，根据方程表示焦点坐标和准线方程；（Ⅱ）设直线l的方程为
（
），与抛物线方程联立，得到根与系数的关系，直线ON的方程为
，联立求得点
的坐标
，证明
.
试题解析：解：（Ⅰ）由抛物线C：
过点P（1，1），得
.
所以抛物线C的方程为.
抛物线C的焦点坐标为（，0），准线方程为.
（Ⅱ）由题意，设直线l的方程为（），l与抛物线C的交点为
，
.
由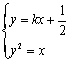
，得
.
则
，
.
因为点P的坐标为（1，1），所以直线OP的方程为
，点A的坐标为
.
直线ON的方程为，点B的坐标为.
因为
，
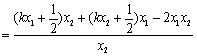
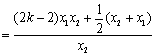
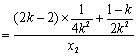
所以
.
故A为线段BM的中点.
【考点】1.抛物线方程；2.直线与抛物线的位置关系
【名师点睛】本题考查了直线与抛物线的位置关系，考查了转换与化归能力，当看到题目中出现直线与圆锥曲
线时，不需要特殊技巧，只要联立直线与圆锥曲线的方程，借助根与系数关系，找准题设条件中突显的或隐含的等量关系，把这种关系“翻译”出来，有时不一定要把结果及时求出来，可能需要整
体代换到后面的计算中去，从而减少计算量.
