设
和
是两个等差数列，记
，
其中
表示
这
个数中最大的数．
（Ⅰ）若
，
，求
的值，并证明
是等差数列；
（Ⅱ）证明：或者对任意正数
，存在正整数
，当
时，
；或者存在正整数，使得
是等差数列．
答案
（Ⅰ）详见解析；（Ⅱ）详见解析.
【解析】
试题分析：（Ⅰ）分别代入求，观察规律，再证明当
时，
，所以
关于
单调递减. 所以
，即证明；（Ⅱ）首先求
的通项公式，分
三种情况讨论证明.
（Ⅱ）设数列
和
的公差分别为
，则
.
所以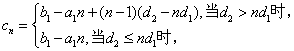
①当
时，取正整数
，则当
时，
，因此
.
此时，
是等差数列.
②当
时，对任意
，
此时，
是等差数列.
③当
时，
当
时，有
.
所以
对任意正数，取正整数
，
故当时，
.
【考点】1.新定义；2.数列的综合应用;3.推理与证明.
【名师点睛】近年北京卷理科压轴题一直为新信息题，本题考查学生对新定义的理解能力和使用能力，本题属于偏难问题，反映出学生对于新的信息的的理解和接受能力，本题考查数列的有关知识及归纳法证明方法，即考查了数列（分段形函数）求值，又考查了归纳法证明和对数据的分析研究，考查了学生的分析问题能力和逻辑推理能力，本题属于拔高难题，特别是第二两步难度较大，适合选拔优秀学生.
