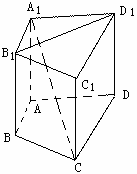
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB;
(3)求三棱锥V-ABC的体积.
答案
证明:(1)如图,因为O,M分别为AB,VA的中点,所以OM∥VB.
因为VB平面MOC,
 所以VB∥平面MOC.
所以VB∥平面MOC.
(2)因为AC=BC,O为![]() AB的中点,
AB的中点,![]() 所以OC⊥AB.
所以OC⊥AB.
因为平面VAB⊥平面ABC,且OC平面ABC,
所以OC⊥平面VAB.
所以平面MOC⊥平面VAB.
(3)在等腰直角三角形ACB中,AC=BC=![]() ,所以AB=2,OC=1,所以S△VAB=
,所以AB=2,OC=1,所以S△VAB=![]() ,
,
又因为OC⊥平面VAB,所以VC-VAB=![]() OC·S△VAB=
OC·S△VAB=![]() .
.
因为三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,所以三棱锥V-ABC的体积为![]() .
.


 。
。  α∩β=l,且P∈l。
α∩β=l,且P∈l。