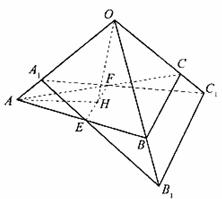
如图,四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.

(I)证明：平面AEC⊥平面AFC；    (II)求二面角B-CE-F的余弦值.

答案

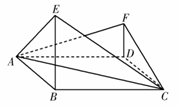
 (I)连接BD，设BDAC=G，连接EG， FG，EF，在菱形ABCD中，不妨设GB=1，由∠ABC=120°，可得AG=GC=.  由BE⊥平面ABCD，AB=BC可知，AE=EC，

又∵AE⊥EC，∴EG=，EG⊥AC，在Rt△EBG中，可得BE=，故DF=.

在Rt△FDG中，可得FG=.

在直角梯形BDFE中，由BD=2，BE=，DF=可得EF=，

∴，∴EG⊥FG，∵AC∩FG=G，∴EG⊥平面AFC，

∵EG面AEC，∴平面AFC⊥平面AEC.

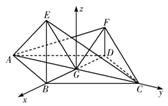
(II)如图，以G为坐标原点，分别以的方向为轴，y轴正方向，为单位长度，建立空间直角坐标系G-xyz，由(Ⅰ)可得B(1，0，0)，E(1,0, )，F(－1,0，)，C(0，，0)，分别求出面BCE与面CEF的法向量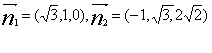

易知，即面BCE面CEF，所以二面角的余弦值为0