给定椭圆
，称圆
为椭圆
的“伴随圆”．已知点
是椭圆
上的点
（1）若过点
的直线
与椭圆
有且只有一个公共点，求被椭圆的伴随圆
所截得的弦长：
（2）
，是椭圆上的两点，设
，
是直线
，
的斜率，且满足
，试问：直线
是否过定点，如果过定点，求出定点坐标，如果不过定点，试说明理由．
【解析】（1）因为点是椭圆上的点．
，
即椭圆
，·······2分
，
，
伴随圆
，
当直线的斜率不存在时：显然不满足与椭圆有且只有一个公共点，·······3分
当直接的斜率存在时：将直线
与椭圆
联立，
得
，
由直线与椭圆有且只有一个公共点得
，
解得
，由对称性取直线
即
，
圆心到直线的距离为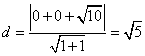
，
直线被椭圆的伴随圆所截得的弦长
，·······6分
（2）设直线，的方程分别为
，
，
设点
，
，
联立得
，
则
得
同理
，·······8分
斜率
，·······9分
同理
，因为，·······10分
所以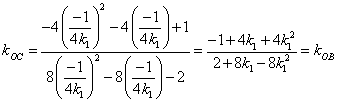
，
，
，三点共线，即直线过定点
．·······12分
曲线的方程的定义：
在直角坐标系中，如果某曲线C（看作点的集合或适合某种条件的点的轨迹）上的点与一个二元方程f（x，y）=0的实数解建立了如下的关系：
（1）曲线上点的坐标都是这个方程的解；
（2）以这个方程的解为坐标的点都是曲线上的点。
那么，这个方程叫做曲线的方程，这条曲线叫做方程的曲线。
求曲线的方程的步骤：
（1）建立适当的坐标系，用有序实数对（x，y）表示曲线上任意一点M的坐标；
（2）写出适合条件的p（M）的集合，P={M|p（M）}；
（3）用坐标表示条件p（M），列出方程f（x，y）=0；
（4）化方程f（x，y）=0为最简形式；
（5）说明化简后的方程的解为坐标的点都在曲线上。
求曲线的方程的步骤：
（1）建立适当的坐标系，用有序实数对（x，y）表示曲线上任意一点M的坐标；
（2）写出适合条件的p（M）的集合，P={M|p（M）}；
（3）用坐标表示条件p（M），列出方程f（x，y）=0；
（4）化方程f（x，y）=0为最简形式；
（5）说明化简后的方程的解为坐标的点都在曲线上。
求曲线方程的常用方法：
（1）待定系数法这种方法需要预先知道曲线的方程，先设出来，然后根据条件列出方程（组）求解未知数。
（2）直译法就是把动点所满足的题设条件直接给表示出来，从而得到其横、纵坐标之间的关系式。（3）定义法就是由曲线的定义直接得到曲线方程。
（4）交轨法：就是在求两动曲线交点轨迹方程时，联立方程组消去参数，得到交点的轨迹方程。在求交点问题时常用此法。
（5）参数法就是通过中间变量找到y、x的间接关系，然后通过消参得出其直接关系。
（6）相关点法就是通过所求动点与已知动点的关系，来求曲线方程的方法。
登录并加入会员可无限制查看知识点解析
B
C
D
