已知函数![]() ,
,![]() ,其中a>1.
,其中a>1.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 在点
在点![]() 处的切线平行,证明
处的切线平行,证明![]() ;
;
(III)证明当![]() 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线.
的切线.
答案
(I)解:由已知,![]() ,有
,有![]() .
.
令![]() ,解得x=0.
,解得x=0.
由a>1,可知当x变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
| x |
| 0 |
|
|
|
| 0 | + |
|
|
| 极小值 |
|
所以函数![]() 的单调递减区间
的单调递减区间![]() ,单调递增区间为
,单调递增区间为![]() .
.
(II)证明:由![]() ,可得曲线
,可得曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
由![]() ,可得曲线
,可得曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
因为这两条切线平行,故有![]() ,即
,即![]() .
.
两边取以a为底的对数,得![]() ,所以
,所以![]() .
.
(III)证明:曲线![]() 在点
在点![]() 处的切线l1:
处的切线l1:![]() .
.
曲线![]() 在点
在点![]() 处的切线l2:
处的切线l2:![]() .
.
要证明当![]() 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,只需证明当
的切线,只需证明当![]() 时,存在
时,存在![]() ,
,![]() ,使得l1和l2重合.
,使得l1和l2重合.
即只需证明当![]() 时,方程组
时,方程组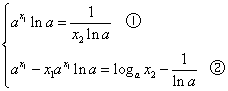 有解,
有解,
由①得![]() ,代入②,得
,代入②,得![]() . ③
. ③
因此,只需证明当![]() 时,关于x1的方程③有实数解.
时,关于x1的方程③有实数解.
设函数![]() ,即要证明当
,即要证明当![]() 时,函数
时,函数![]() 存在零点.
存在零点.
![]() ,可知
,可知![]() 时,
时,![]() ;
;![]() 时,
时,![]() 单调递减,又
单调递减,又
![]() ,
,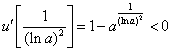 ,故存在唯一的x0,且x0>0,使得
,故存在唯一的x0,且x0>0,使得![]() ,即
,即
![]() .
.
由此可得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减. ![]() 在
在![]() 处取得极大值
处取得极大值![]() .
.
因为![]() ,故
,故![]() ,
,
所以![]() .
.
下面证明存在实数t,使得![]() .
.
由(I)可得![]() ,
,
当![]() 时,
时,
有![]() ,
,
所以存在实数t,使得![]()
因此,当![]() 时,存在
时,存在![]() ,使得
,使得![]() .
.
所以,当![]() 时,存在直线l,使l是曲线
时,存在直线l,使l是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线.
的切线.

 表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用
表示,我们把这个式子称为函数f(x)从x1到x2的平均变化率,习惯上用 表示,即平均变化率
表示,即平均变化率
 的值可正可负,但
的值可正可负,但 不为0.f(x)为常数函数时,
不为0.f(x)为常数函数时,
 这段时间内,当
这段时间内,当 时平均速度的极限,即
时平均速度的极限,即
 当d趋于0时的极限.
当d趋于0时的极限. ,我们称它为函数y=f(x)在x=x0处的导数,记作
,我们称它为函数y=f(x)在x=x0处的导数,记作 或
或 ,即
,即 。
。
 。
。 时的极限值.
时的极限值. 时,比值
时,比值 的极限存在,则f(x)在点x0处可导;若
的极限存在,则f(x)在点x0处可导;若 可以为正,也可以为负,还可以时正时负,但
可以为正,也可以为负,还可以时正时负,但 .而函数的增量
.而函数的增量 可正可负,也可以为0.
可正可负,也可以为0.


 与原来的函数f(x)有相同的定义域(a,b),且导函数
与原来的函数f(x)有相同的定义域(a,b),且导函数