已知椭圆![]() .
.
(Ⅰ)我们知道圆具有性质:若![]() 为圆O:
为圆O:![]() 的弦AB的中点,则直线AB的斜率
的弦AB的中点,则直线AB的斜率![]() 与直线OE的斜率
与直线OE的斜率![]() 的乘积
的乘积![]() 为定值。类比圆的这个性质,写出椭圆
为定值。类比圆的这个性质,写出椭圆![]() 的类似性质,并加以证明;
的类似性质,并加以证明;
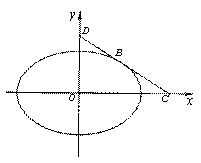
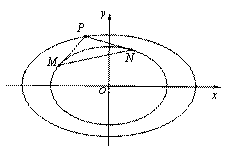
(Ⅱ)如图(1),点B为![]() 在第一象限中的任意一点,过B作
在第一象限中的任意一点,过B作![]() 的切线
的切线![]() ,
,![]() 分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值;
分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值;
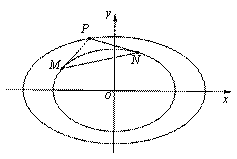
(Ⅲ)如图(2),过椭圆![]() 上任意一点
上任意一点![]() 作
作![]() 的两条切线PM和PN,切点分别为M,N.当点P在椭圆
的两条切线PM和PN,切点分别为M,N.当点P在椭圆![]() 上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
 |
图(1) 图(2)
答案
解:(Ⅰ)若A,B为椭圆![]() 上相异的两点,
上相异的两点,![]() 为A,B中点,当直线AB
为A,B中点,当直线AB
 的斜率
的斜率![]() 与直线OP的斜率
与直线OP的斜率![]() 的乘积
的乘积![]() 必为定值;----- -------------1分
必为定值;----- -------------1分
证1:设![]() ,则
,则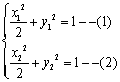
(2)-(1)得:![]() ,-----------2分
,-----------2分
![]() 仅考虑斜率存在的情况
仅考虑斜率存在的情况![]() :
:![]()
![]() ----------------------------------------4分
----------------------------------------4分
证2:设AB:![]() 与椭圆
与椭圆![]() 联立得:
联立得:![]()
![]() , --------------2分
, --------------2分
所以![]()
![]() ----------4分
----------4分
(Ⅱ)(ⅰ)当点A无限趋近于点B时,割线AB的斜率就等于椭圆上的B的切线的斜率![]() ,
,
即![]() ,
,![]()
所以点B处的切线QB:![]() ----------------6分
----------------6分
令![]() ,
,![]() ,令
,令![]() ,所以
,所以![]() -----------------8分
-----------------8分
又点B在椭圆的第一象限上,所以![]()
![]()
![]() ,当且仅当
,当且仅当![]()
所以当![]() 时,三角形OCD的面积的最小值为
时,三角形OCD的面积的最小值为![]() -------10分(没写等号成立扣1分)
-------10分(没写等号成立扣1分)
(ⅱ)设![]() ,由(ⅰ)知点
,由(ⅰ)知点![]() 处的切线为:
处的切线为:![]()
又![]() 过点
过点![]() ,所以
,所以![]() ,又可理解为点
,又可理解为点![]() 在直线
在直线![]() 上
上
 同理点
同理点![]() 在直线
在直线![]() 上,所以直线MN的方程为:
上,所以直线MN的方程为:![]() --------------------------12分
--------------------------12分
所以原点O到直线MN的距离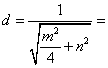
![]() ,----------13分
,----------13分
所以直线MN始终与圆![]() 相切. ------------------------14分
相切. ------------------------14分

