已知![]() 是无穷数列.给出两个性质:
是无穷数列.给出两个性质:
①对于![]() 中任意两项
中任意两项![]() ,在
,在![]() 中都存在一项
中都存在一项![]() ,使
,使![]() ;
;
②对于![]() 中任意项
中任意项![]() ,在
,在![]() 中都存在两项
中都存在两项![]() .使得
.使得![]() .
.
(Ⅰ)若![]() ,判断数列
,判断数列![]() 是否满足性质①,说明理由;
是否满足性质①,说明理由;
(Ⅱ)若![]() ,判断数列
,判断数列![]() 是否同时满足性质①和性质②,说明理由;
是否同时满足性质①和性质②,说明理由;
(Ⅲ)若![]() 是递增数列,且同时满足性质①和性质②,证明:
是递增数列,且同时满足性质①和性质②,证明:![]() 为等比数列.
为等比数列.
答案
(Ⅰ)详见解析;(Ⅱ)详解解析;(Ⅲ)证明详见解析.
【解析】
【分析】
(Ⅰ)根据定义验证,即可判断;
(Ⅱ)根据定义逐一验证,即可判断;
(Ⅲ)解法一:首先,证明数列中的项数同号,然后证明![]() ,最后,用数学归纳法证明数列为等比数列即可.
,最后,用数学归纳法证明数列为等比数列即可.
解法二:首先假设数列中的项数均为正数,然后证得![]() 成等比数列,之后证得
成等比数列,之后证得![]() 成等比数列,同理即可证得数列为等比数列,从而命题得证.
成等比数列,同理即可证得数列为等比数列,从而命题得证.
【详解】(Ⅰ)![]() 不具有性质①;
不具有性质①;
(Ⅱ)![]() 具有性质①;
具有性质①;
![]() 具有性质②;
具有性质②;
(Ⅲ)【解法一】
首先,证明数列中的项数同号,不妨设恒为正数:
显然![]() ,假设数列中存在负项,设
,假设数列中存在负项,设![]() ,
,
第一种情况:若![]() ,即
,即![]() ,
,
由①可知:存在![]() ,满足
,满足![]() ,存在
,存在![]() ,满足
,满足![]() ,
,
由![]() 可知
可知![]() ,从而
,从而![]() ,与数列的单调性矛盾,假设不成立.
,与数列的单调性矛盾,假设不成立.
第二种情况:若![]() ,由①知存在实数
,由①知存在实数![]() ,满足
,满足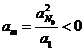 ,由
,由![]() 的定义可知:
的定义可知:![]() ,
,
另一方面,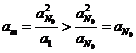 ,由数列
,由数列![]() 单调性可知:
单调性可知:![]() ,
,
这与![]() 的定义矛盾,假设不成立.
的定义矛盾,假设不成立.
同理可证得数列中的项数恒为负数.
综上可得,数列中的项数同号.
其次,证明![]() :
:
利用性质②:取![]() ,此时
,此时![]() ,
,
由数列的单调性可知![]() ,
,
而![]() ,故
,故![]() ,
,
此时必有![]() ,即
,即![]() ,
,
最后,用数学归纳法证明数列为等比数列:
假设数列![]() 的前
的前![]() 项成等比数列,不妨设
项成等比数列,不妨设![]() ,
,
其中![]() ,(
,(![]()
![]() 情况类似)
情况类似)
由①可得:存在整数![]() ,满足
,满足![]() ,且
,且![]() (*)
(*)
由②得:存在![]() ,满足:
,满足:![]() ,由数列的单调性可知:
,由数列的单调性可知:![]() ,
,
由![]() 可得:
可得:![]() (**)
(**)
由(**)和(*)式可得:![]() ,
,
结合数列的单调性有:![]() ,
,
注意到![]() 均为整数,故
均为整数,故![]() ,
,
代入(**)式,从而![]() .
.
总上可得,数列![]() 的通项公式为:
的通项公式为:![]() .
.
即数列![]() 为等比数列.
为等比数列.
【解法二】假设数列中的项数均为正数:
首先利用性质②:取![]() ,此时
,此时![]() ,
,
由数列的单调性可知![]() ,
,
而![]() ,故
,故![]() ,
,
此时必有![]() ,即
,即![]() ,
,
即![]() 成等比数列,不妨设
成等比数列,不妨设![]() ,
,
然后利用性质①:取![]() ,则
,则![]() ,
,
即数列中必然存在一项的值为![]() ,下面我们来证明
,下面我们来证明![]() ,
,
否则,由数列的单调性可知![]() ,
,
在性质②中,取![]() ,则
,则![]() ,从而
,从而![]() ,
,
与前面类似的可知则存在![]() ,满足
,满足![]() ,
,
若![]() ,则:
,则:![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则:
,则:![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则:
,则:![]() ,与数列的单调性矛盾;
,与数列的单调性矛盾;
即不存在满足题意的正整数![]() ,可见
,可见![]() 不成立,从而
不成立,从而![]() ,
,
同理可得:![]() ,从而数列
,从而数列![]() 为等比数列,
为等比数列,
同理,当数列中的项数均为负数时亦可证得数列为等比数列.
由推理过程易知数列中的项要么恒正要么恒负,不会同时出现正数和负数.
从而题中的结论得证,数列![]() 为等比数列.
为等比数列.
【点睛】本题主要考查数列的综合运用,等比数列的证明,数列性质的应用,数学归纳法与推理方法、不等式的性质的综合运用等知识,意在考查学生的转化能力和推理能力.
