已知函数
．若函数
在
处有极值-4．
（1）求的单调递减区间；
（2）求函数在
上的最大值和最小值．
答案
（1）
；（2）
.
【解析】
先求出导函数，根据导数的几何意义得到关于
的方程组，求得后再根据导函数的符号求出单调递减区间．
由求出函数的单调区间，可以数判断函数
在
上的单调性，求出函数在上的极值和端点值，通过比较可得的最大值和最小值．
试题解析：
（1）∵
，
∴
，
依题意有即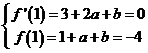
，解得
∴
，
由
，得
，
∴函数
单调递减区间
由知
∴
，
令
，解得
．
当
变化时，
的变化情况如下表：
由上表知，函数在
上单调递减，在
上单调递增．
故可得
又
．
∴
综上可得函数在上的最大值和最小值分别为
和
．
，则f在[a，b]上可积，且
，这称为牛顿-莱布尼茨公式，它也常写成
。
