已知α∈
，且
.
(1)求cos α的值；(2)若sin(α－β)＝－
，β∈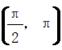
，求cos β的值．
答案
解：（1）∵α∈（
，π），且sin
+cos＝
，两边平方可得：1+sinα＝
，∴sinα＝
，可得：cosα＝﹣
＝﹣
．
（2）∵由（1）可得：sin α＝
，cosα＝﹣
．
∵
＜α＜π，＜β＜π，∴﹣＜α﹣β＜，
又sin（α﹣β）＝﹣
，得cos（α﹣β）＝
，
∴cos β＝cos[α﹣（α﹣β）]＝cosαcos（α﹣β）+sinαsin（α﹣β）＝﹣×+×（﹣）＝﹣
．
”
(k
(k
(k
=(sin
,2cos
=(
)
, sin
