设椭圆![]() 的焦点为
的焦点为![]() ,
,![]() 是椭圆上一点,且
是椭圆上一点,且![]() ,若
,若![]() 的外接圆和内切圆的半径分别为
的外接圆和内切圆的半径分别为![]() ,当
,当![]() 时,椭圆的离心率为( )
时,椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案
B
【解析】
分析:
详解:由椭圆![]() 的焦点为
的焦点为![]()
![]() 为椭圆上一点,且
为椭圆上一点,且![]() ,有
,有![]() 根据正弦定理
根据正弦定理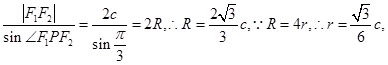 由余弦定理,
由余弦定理,![]() 由
由![]()
![]() ,可得
,可得![]() ,则由三角形面积公式
,则由三角形面积公式![]() 可得
可得![]()
故选B.
点睛:本题考查椭圆的离心率的求法,注意运用椭圆的定义和三角形的内切圆的半径的求法,以及正弦定理,余弦定理的应用,考查化简整理的运算能力,是中档题.