如图，在四棱锥 P - ABCD 中，底面 ABCD 为平行四边形， △ PCD 为等边三角形，平面 PAC ⊥ 平面 PCD ， PA ⊥ CD ， CD =2 ， AD =3.

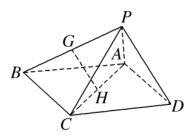
（ 1 ）设 G ， H 分别为 PB ， AC 的中点，求证 ∶ GH // 平面 PAD ；

（ 2 ）求证 ∶ PA ⊥ 平面 PCD ； .

（ 3 ）求直线 AD 与平面 PAC 所成角的正弦值 .

答案

（ 1 ）证明见解析；（ 2 ）证明见解析；（ 3 ） .

【分析】

（ 1 ）构造中位线得到线线平行，从而证明线面平行；

（ 2 ）取棱 PC 的中点 N ，连接 DN ，得 DN ⊥ PC ，进一步得 DN ⊥ 平面 PAC .

又 PA ⊥ CD ， 从而可得 PA ⊥ 平面 PCD ；

（ 3 ）由 DN ⊥ 平面 PAC ，可知 ∠ DAN 为直线 AD 与平面 PAC 所成的角，再解三角形即可 .

【详解】

（ 1 ）证明 ∶ 连接 BD ，易知 ， BH = DH .

又由 BG = PG ，故 GH // PD .

又因为 平面 PAD ， 平面 PAD ，所以 GH // 平面 PAD .

（ 2 ）证明 ∶ 取棱 PC 的中点 N ，连接 DN . 依题意，得 DN ⊥ PC .

又因为平面 PAC ⊥ 平面 PCD ，平面 PAC ∩ 平面 PCD = PC ，

所以 DN ⊥ 平面 PAC .

又 平面 PAC ，所以 DN ⊥ PA .

又已知 PA ⊥ CD ， ，

所以 PA ⊥ 平面 PCD .

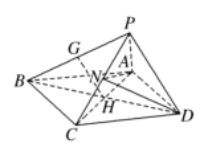
（ 3 ）连接 AN ，由（ 2 ）中 DN ⊥ 平面 PAC ，可知 ∠ DAN 为直线 AD

与平面 PAC 所成的角 .

因为 △ PCD 为等边三角形， CD =2 且 N 为 PC 的中点，

所以 DN =

又 DN ⊥ AN ，在 中， .

所以，直线 AD 与平面 PAC 所成角的正弦值为