新冠肺炎疫情发生以来,我国某科研机构开展应急科研攻关,研制了一种新型冠状病毒疫苗,并已进入二期临床试验 . 根据普遍规律,志愿者接种疫苗后体内会产生抗体,人体中检测到抗体,说明有抵御病毒的能力 . 通过检测,用 表示注射疫苗后的天数,
表示人体中抗体含量水平(单位:
,即:百万国际单位 / 毫升),现测得某志愿者的相关数据如下表所示:
| 天数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 抗体含量水平 | 5 | 10 | 26 | 50 | 96 | 195 |
根据以上数据,绘制了散点图 .
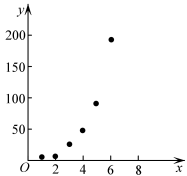
(1) 根据散点图判断, 与
( a , b , c , d 均为大于 0 的实数)哪一个更适宜作为描述 y 与 x 关系的回归方程类型?(给出判断即可,不必说明理由)
(2) 根据( 1 )的判断结果求出 y 关于 x 的回归方程,并预测该志愿者在注射疫苗后的第 10 天的抗体含量水平值;
(3) 从这位志愿者的前 6 天的检测数据中随机抽取 4 天的数据作进一步的分析,记其中的 y 值大于 50 的天数为 X ,求 X 的分布列与数学期望 .
参考数据:
| | | | | | | | |
| 3.50 | 63.67 | 3.49 | 17.50 | 9.49 | 12.95 | 519.01 | 4023.87 |
其中 . 参考公式:用最小二乘法求经过点
,
,
,
,
的线性回归方程
的系数公式,
;
.
答案
(1)
(2) , 4023.87
(3) 分布列答案见解析,数学期望:
【解析】
【分析】
( 1 )由于这些点分布在一条曲线的附近,从而可选出回归方程,
( 2 )设 ,
,则建立 w 关于 x 的回归方程
,然后根据公式和表中的数据求解回归方程即可,再将
代入回归方程可求得在注射疫苗后的第 10 天的抗体含量水平值,
( 3 )由题意可知 x 的可能取值为 0 , 1 , 2 ,然后求对应的概率,从而可求出分布列和期望
(1)
根据散点图可知这些点分布在一条曲线的附近,所以 更适合作为描述 y 与 x 关系的回归方程类型 .
(2)
设 ,变换后可得
,
设 ,建立 w 关于 x 的回归方程
,
,
所以
所以 w 关于 x 的回归方程为 ,
所以 ,
当 时,
,
即该志愿者在注射疫苗后的第 10 天的抗体含量水平值约为 4023.87 miu / mL .
(3)
由表格数据可知,第 5 , 6 天的 y 值大于 50 ,
故 x 的可能取值为 0 , 1 , 2 ,
,
,
,
X 的分布列为
| | 0 | 1 | 2 |
| | | | |
.

 。
。 ;在整个抽样过程中各个个体被抽到的概率为
;在整个抽样过程中各个个体被抽到的概率为 ;
;