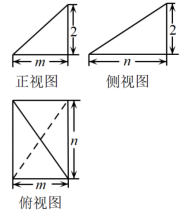
如图是一个简单几何体的三视图，若 m + n =4 ，则该几何体体积的最大值为（ ）

A ． B ． C ． 4 D ． 8

答案

A

【解析】

【分析】

还原给定的三视图对应的几何体，求出体积表达式，再利用二次函数求出最大值作答 .

【详解】

依题意，原三视图对应的几何体是三棱锥 ，如图， ，其高为 2 ，

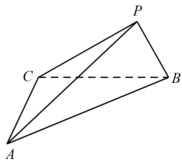
而 ，则三棱锥 的体积 ，

显然 ，则当 时， ，

所以该几何体体积的最大值为 .

故选： A