已知函数 ，若方程 有 5 个不同的实数解，则实数 a 的取值范围为（ ）

A ． B ． C ． D ．

答案

D

【解析】

【分析】

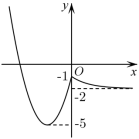
画出函数 的大致图象，令 ，方程 有 5 个不同的实数解，转化为 根的分布问题，分情况讨论即可 .

【详解】

函数 的大致图象如图所示，对于方程 有 5 个不同的实数解，

令 ，则 在 ， 上各有一个实数解或 的一个解为 -1 ，另一个解在 内或 的一个解为 -2 ，另一个解在 内 .

当 在 ， 上各有一个实数解时，设 ，则 解得 ；

当 的一个解为 -1 时， ，此时方程的另一个解为 -3 ，不在 内，不满足题意；

当 的一个解为 -2 时， ，此时方程的另一个解为 ，在 内，满足题意 .

综上可知，实数 a 的取值范围为 .

故选： D.