埃拉托斯特尼是古希腊亚历山大时期著名的地理学家，他最出名的工作是计算了地球（大圆）的周长 . 如图，在赛伊尼，夏至那天中午的太阳几乎正在天顶方向（这是从日光直射进该处一井内而得到证明的） . 同时在亚历山大城（该处与赛伊尼几乎在同一子午线上），其天顶方向与太阳光线的夹角测得为 . 因太阳距离地球很远，故可把太阳光线看成是平行的 . 埃拉托斯特尼从商队那里知道两个城市间的实际距离大概是 5000 斯塔蒂亚，按埃及的长度算， 1 斯塔蒂亚等于 157.5 米，则埃拉托斯特尼所测得地球的周长约为（ ）

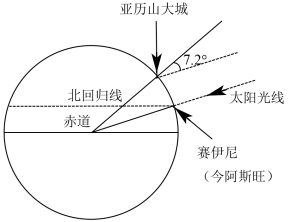
A ． 38680 千米 B ． 39375 千米 C ． 41200 千米 D ． 42192 千米

答案

B

【分析】由题意可将赛伊尼和亚历山大城之间的距离看作圆心角为 的扇形的弧长，由此可计算地球半径，进而求得地球周长 .

【详解】由题意可知，赛伊尼和亚历山大城之间的距离可看作圆心角为 的扇形的弧长，

设地球半径为 ，则 ，

∴ 地球周长为 （米） = （千米），

故选： B.