已知函数 ， 图象向左平移 个单位后关于直线 对称，则下列说法正确的是（ ）

A ．在区间 上有一个零点 B ．关于 对称

C ．在区间 上单调递增 D ．在区间 上的最大值为 2

答案

A

【分析】通过函数 的平移变换后图象关于直线 对称可求得 值，从而可求出函数解析式，然后使用换元法画出函数图象，再逐项判断即可 .

【详解】函数 ， 图象向左平移 个单位后的图象对应的解析式为： ；

而 图象关于直线 对称，且 ，于是 ， ；

；

，所以 不关于 对称，故 B 错误；

当 时，则 ，令 ，则 ，此时函数图象如图 :

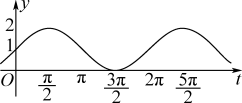
结合图象可知，当 时，即 ， 与坐标轴只有一个交点，即 只有一个零点，故 A 正确；

当 时，则 ，结合图象可知，此时 有增有减，故 C 错误；

当 时，则 ，结合图象可知，此时 单调递增，所以，当 时，即 ，函数取最大值， ，故 D 错误；

故选： A.