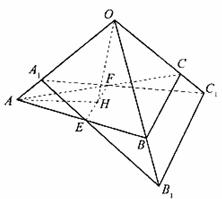
如图，在正方体 中，点 是线段 上的动点，则下列说法错误的是（ ）

A ．当点 移动至 中点时，直线 与平面 所成角最大且为

B ．无论点 在 上怎么移动，都有

C ．当点 移动至 中点时，才有 与 相交于一点，记为点 ，且

D ．无论点 在 上怎么移动，异面直线 与 所成角都不可能是

答案

A

【分析】建立空间直角坐标系，借助空间向量研究直线与直线垂直、夹角问题的相关公式和结论，结合函数的性质可判断选项 A 、 B 、 D ；由三角形的相似关系可判断选项 C ．

【详解】以 为坐标原点， ， ， 所在直线分别为 x 轴， y 轴， z 轴，建立空间直角坐标系，如图，

设正方体的棱长为 1 ，则

∵ 点 是线段 上的动点， ∴ 可设 ， ，

∴ ， ， ，

设 是平面 的一个法向量，则 ，即 ，

令 ，则 ，

设直线 与平面 所成角为 ，则

∴ 当 时， 取最大值 ，即当点 移动至 中点时 最大，

由于 ，则 的最大值大于 ，故 A 错误；

∵ ， ，

∴ ，

∴ 无论点 在 上怎么移动，都有 ，故 B 正确；

若 不是 的中点，则 与 是异面直线；当 为 的中点时，也是 的中点， 与 均在平面 内且必相交，所以当点 移动至 中点时，才有 与 相交于一点，记为点 ，连 和 ，如图，

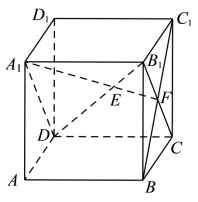
根据 ， 可得 ＝ ＝ 2 ，故 C 正确；

∵ ，

设异面直线 与 所成角为 ，则

， ∴ ，故 D 正确．

故选： A ．