定义在 上的函数 满足 ， ；且当 时， ．则方程 所有的根之和为（ ）

A ． 6 B ． 12 C ． 14 D ． 10

答案

D

【分析】根据题意可得 为奇函数，关于直线 对称且周期为 4 ，再根据当 时， ，求导分析单调性，从而画出简图，根据函数的性质求解零点和即可 .

【详解】 ∵ ， ∴ 为奇函数，又 ∵ ， ∴ 关于直线 对称．

当 时， ， 单调递增， ， 一个周期为 4 ， 关于 中心对称．

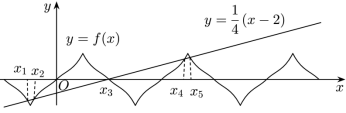
由 ， ∴ 所有实根之和为 .

故选： D ．

【点睛】本题求零点之和需要掌握的方法：

（ 1 ）函数的性质运用：根据条件中函数满足的关系式推导函数的奇偶性、对称性、周期性和在区间内的单调性，并运用性质求零点和；

（ 2 ）数形结合：根据给定区间的函数解析式作图，再根据函数的性质补全剩余图象；