自行车停放时将后轮旁边的撑子放下,自行车就停稳了,这里用到了( )
A .两条平行直线确定一个平面
B .两条相交直线确定一个平面
C .不共线的三点确定一个平面
D .三点确定一个平面
C
【分析】
结合确定一个平面的方法确定正确选项 .
【详解】
自行车的前后轮与脚撑分别接触地面,使得自行车稳定,
此时自行车与地面的三个接触点不在同一条线上,即不共线的三点确定一个平面.
故选: C .
三棱锥的 6 条棱中,异面直线有( )
A . 4 对 B . 3 对 C . 2 对 D . 1 对
B
【分析】
结合异面直线的知识确定正确选项 .
【详解】
考虑三棱锥 ABCD ,可得直线 AB 与直线 CD 、直线 AC 与直线 BD 、
直线 AD 与直线 BC 均为异面直线,共三对.
故选: B

下列判断正确的是( )
A .正三棱锥一定是正四面体
B .底面是正方形的四棱锥是正四棱锥
C .底面是正方形的直四棱柱是正四棱柱
D .底面是正方形的棱台是正四棱台
C
【分析】
由正四面体、正四棱锥、正四棱柱、正四棱台的定义辨析,即可判断
【详解】
正三棱锥不一定是正四面体,侧棱长与底面边长可能不相等,故 A 错误;
底面是正方形的四棱锥不一定是正四棱锥,顶点在底面的射影不一定是底面的中心,故 B 错误;
由正四棱住的概念可知,底面是正方形的直四棱柱是正四棱柱,故 C 正确;
底面是正方形的棱台不一定是正四棱台,原因是棱台的侧棱延长后的交点在两底面的射影不一定为正方形的中心,故 D 错误.
故选: C
如图是一个无盖的正方体盒子展开后的平面图, A , B , C 是展开图上的三点,则在正方体盒子中, ∠ ABC 的度数为( )
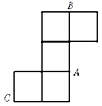
A . 30° B . 45° C . 60° D . 90°
D
【分析】
还原为正方体,如图所示,然后利用由正方体的性质求解即可
【详解】
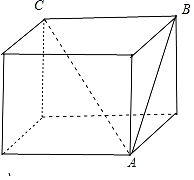
还原为正方体,如图所示:
由正方体的性质可知, CB ⊥ 平面 AB ,
所以 CB ⊥ AB ,即 ∠ ABC = 90° ,
故选: D .
已知 l , m , n 为三条不同的直线, α , β 为两个不同的平面,则下列命题中正确的是( )
A .若 l ⊥ m , l ⊥ n ,且 m , n ⊂α ,则 l ⊥α
B .若 m ∥β , n ∥β ,且 m , n ⊂α ,则 α∥β
C .若 m ∥ n , n ⊂α ,则 m ∥α
D .若 l ⊥β , l ⊂α ,则 α⊥β
D
【分析】
根据空间线线、线面、面面的位置关系有关知识对选项进行分析,由此确定正确选项 .
【详解】
对于 A :若 l ⊥ m , l ⊥ n ,且 m , n ⊂α ,若 m 和 n 为相交直线,才有 l ⊥α ,故 A 错误;
对于 B :若 m ∥β , n ∥β ,且 m 和 n 为相交直线, m , n ⊂α ,才有 α∥β ,故 B 错误;
对于 C :若 m ∥ n , m ⊄α ,且 n ⊂α ,才有 m ∥α ,故 C 错误;
对于 D :若 l ⊥β , l ⊂α ,根据面面垂直的判定,则 α⊥β ,故 D 正确;
故选: D .
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户刘潘分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。