2021-2022学年度高中数学函数的应用练习题含解析
高中
整体难度：中等
2022-08-02
题号
一
二
三
四
五
评分
一、选择题 (共15题)
添加该题型下试题
1.
生物体死亡后，它机体内原有的碳 14 含量 C 会按确定的比率衰减（称为衰减率）， C 与死亡年数 t 之间的函数关系式为 （ k 为常数），大约每经过 5730 年衰减为原来的一半，这个时间称为 “ 半衰期 ” ．若 2022 年某遗址文物出土时碳 14 的残余量约为原始量的 85% ，则可推断该文物属于（ ）
参考数据： ；参考时间轴：
A ．战国 B ．汉 C ．唐 D ．宋
难度：
知识点：基本初等函数I
使用次数：153
【答案】
C
【解析】
【分析】
根据 “ 半衰期 ” 求得 ，进而解方程
，求得
，从而可推断出该文物所属朝代 .
【详解】
解：当 时，
，故
，解得
，所以
，
由题意得 ，
，解得
，
而 ，可推断该文物属于唐 .
故选： C ．
2.
已知函数 ，若方程
有 5 个不同的实数解，则实数 a 的取值范围为（ ）
A ． B ．
C ．
D ．
难度：
知识点：基本初等函数I
使用次数：221
【答案】
D
【解析】
【分析】
画出函数 的大致图象，令
，方程
有 5 个不同的实数解，转化为
根的分布问题，分情况讨论即可 .
【详解】
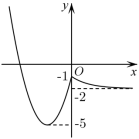
函数 的大致图象如图所示，对于方程
有 5 个不同的实数解，
令 ，则
在
，
上各有一个实数解或
的一个解为 -1 ，另一个解在
内或
的一个解为 -2 ，另一个解在
内 .
当 在
，
上各有一个实数解时，设
，则
解得
；
当 的一个解为 -1 时，
，此时方程的另一个解为 -3 ，不在
内，不满足题意；
当 的一个解为 -2 时，
，此时方程的另一个解为
，在
内，满足题意 .
综上可知，实数 a 的取值范围为 .
故选： D.
3.
设 ，已知关于 x 的方程
恰有 6 个不同的实数根，则 k 的取值范用为（ ）
A ．（ -2 ， 0 ） B ．（ -3 ， -2 ） C ．［ -3 ， -2 ） D ．［ -2 ， 0 ）
难度：
知识点：函数的应用
使用次数：252
【答案】
B
【解析】
【分析】
设关于 的方程
的两个根分别为
，由关于
的方程
恰好有 6 个不同的实数根，等价于关于
的图象与
公有 6 个交点，结合图象即可求解 .
【详解】
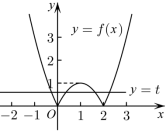
的图象如图所示，令
，设关于
的方程
的两个根分别为
，由关于
的方程
恰好有 6 个不同的实数根，等价于关于
的图象与
公有 6 个交点，由图可知：
或者
，设
，当
时，则
；
当 ，
则
不符合要求；
故
故选： B
4.
已知函数 ，若方程
有 5 个不同的实数解，则
的范围是（ ）
A ． B ．
C ． D ．
难度：
知识点：基本初等函数I
使用次数：289
【答案】
A
【解析】
【分析】
解方程 得
或
，根据
的取值分类讨论即可 .
【详解】
方程 ，解得
或
，
若 ，
，
解得 或 0 或 2 ，不符合题意，所以
，
由 ，可得原方程有 3 个不等实根
或 0 或 2 ；
所以只要 有 2 个不等实根即可．
由 可得
，
即有 ，
综上可得 ．
故选： A ．
5.
函数 的零点个数是（ ）
A ． 1 B ． 2 C ． 3 D ． 4
难度：
知识点：导数及其应用
使用次数：116
【答案】
B
【解析】
【分析】
令 ，即可得到
，则函数的零点个数转化为函数
与
的交点个数，画出函数图象，数形结合即可判断 .
【详解】
解：由题意，令 ，即
，
则函数 的零点个数，等价于两个函数
与
的交点个数，
与
两函数的图象如下图所示：
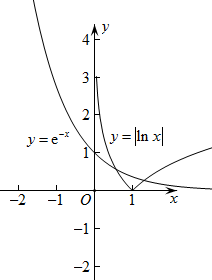
由图知，两个函数有 个交点，故函数
的零点个数是
.
故选： B ．
本卷还有30题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
35
总体难度：
中等
难度统计
难度系数
数量
占比
中等
13
37.14%
容易
10
28.57%
偏难
7
20.0%
很难
1
2.85%
基础
4
11.42%
题型统计
大题类型
数量
占比
选择题
15
42.85%
填空题
10
28.57%
解答题
5
14.28%
未分类
5
14.28%
知识点统计
知识点
数量
占比
基本初等函数I
29
82.85%
函数的应用
2
5.71%
导数及其应用
1
2.85%
三角函数
2
5.71%
集合与函数的概念
1
2.85%
版权提示
该作品由: 用户星屑分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。