2021-2022学年度高中数学数列练习题含解析
高中
整体难度：中等
2022-08-08
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
在等比数列 中，
，则其前 3 项的和
的取值范围是（ ）
A ． B ．
C ．
D ．
难度：
知识点：数列
使用次数：137
【答案】
C
【解析】
【分析】
把 用公比
表示，利用函数知识得结论．
【详解】
设 的公比为
，则
，
，
时等号成立，
与
时都有
，所以
．
故选： C ．
2.
已知数列 满足
，且
，则
（ ）
A ． B ．
C ．
D ．
难度：
知识点：数列
使用次数：296
【答案】
B
【解析】
【分析】
根据题中的递推关系式及 ，依次取
，
，
，
可分别求出
，
，
，
的值，即可求得答案 .
【详解】
由题意得 ，又
，所以
，
易得 ，则
，
同理， ，
，故
故选： B
3.
已知数列 { } 满足
，则
（ ）
A ． B ．
C ．
D ．
难度：
知识点：数列
使用次数：249
【答案】
C
【解析】
【分析】
先由 判断出
是递增数列且
，再由
结合累加法求得
；再由
结合累加法求得
，即可求解 .
【详解】
由 ，得
，
，所以
，又
，
所以数列 是递增数列且
，
，所以
，
所以
，
所以 ，
. 当
，得
，由
得
，
则 ，
同上由累加法得 ，
所以 ，所以
，则
.
故选： C.
【点睛】
解决数列中的范围问题，通常借助放缩法进行求解 . 本题由 得出
是递增数列且
，进而由
结合累加法求得结果 .
4.
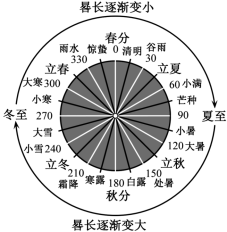
我国古代数学著作《周髀算经》中记载了二十四节气与晷长的关系：每个节气的晷长损益相同 . 晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度，如图 1 所示，损益相同，即相邻两个节气晷长减少或增加的量相同，且周而复始 . 二十四节气及晷长变化如图 2 所示 . 已知谷雨时节晷长为 5.5 尺，霜降时节晷长为 9.5 尺，则二十四节气中晷长的最大值为（ ）
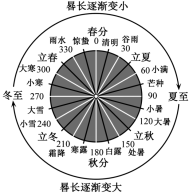
A ． 14.5 B ． 13.5 C ． 12.5 D ． 11.5
难度：
知识点：数列
使用次数：254
【答案】
B
【解析】
【分析】
设相邻两个节气晷长减少或增加的量为 ，由图可知冬至的晷长最大，设为
，从冬至到谷雨减少
，从霜降到冬至增加
，然后根据题意列方程组可求得答案
【详解】
设相邻两个节气晷长减少或增加的量为 ，由图可知冬至的晷长最大，设为
，从冬至到谷雨减少
，从霜降到冬至增加
，则
，解得
，
所以二十四节气中晷长的最大值为 ，
故选： B
5.
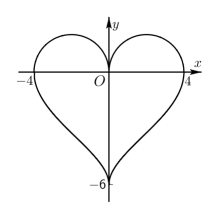
某数学爱好者以函数图像组合如图 “ 爱心 ” 献给在抗疫一线的白衣天使，向他们表达崇高的敬意！爱心轮廓是由曲线 与
构成，若 a ，
， c 依次成等比数列，则
（ ）
A ． B ．
C ．
D ．
难度：
知识点：数列
使用次数：134
【答案】
A
【解析】
【分析】
由 “ 爱心 ” 图 经过点
, 可求出
，再由 “ 爱心 ” 图
过点
与
，可求出
，再由 a ，
， c ，依次成等比数列可得
代入即可求出答案 .
【详解】
解：由 “ 爱心 ” 图知 经过点
，
即 ，
．
由 “ 爱心 ” 图知 必过点
与
，
所以 ，得
，
，
若 a ， ， c ，依次成等比数列，则
，
从而 ，所以
．
故选 :A ．
本卷还有30题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
35
总体难度：
中等
难度统计
难度系数
数量
占比
容易
13
37.14%
基础
6
17.14%
偏难
1
2.85%
中等
15
42.85%
题型统计
大题类型
数量
占比
选择题
10
28.57%
未分类
5
14.28%
填空题
15
42.85%
解答题
5
14.28%
知识点统计
知识点
数量
占比
数列
33
94.28%
函数的应用
1
2.85%
基本初等函数I
1
2.85%
版权提示
该作品由: 用户小寒分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。