2022-2023学年度高中数学空间向量与立体几何练习题含解析
高中
整体难度：中等
2022-08-29
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
已知向量 ，
，且
与
互相垂直，则
的值是（ ）
A ．－ 1 B ． C ．
D ．
难度：
知识点：空间中的向量与立体几何
使用次数：263
【答案】
D
【分析】先求出 与
的坐标，再由
与
互相垂直，可得
，从而可求出
的值 .
【详解】因为 ，
，
所以 ，
，
因为 与
互相垂直，
所以 ，解得
，
故选： D
2.
如图，平行六面体 中，
与
的交点为
，设
，
，
，则选项中与向量
相等的是（ ）
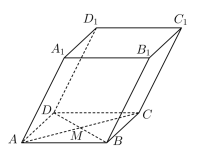
A ． B ．
C ． D ．
难度：
知识点：平面向量
使用次数：224
【答案】
A
【分析】根据空间向量线性运算法则计算可得 .
【详解】解：平行六面体 中，
与
的交点为
，设
，
，
，
所以 ，
则 ，
所以 ．
故选： A ．
3.
已知向量 是空间的一个基底，向量
是空间的另一个基底，一向量
在基底
下的坐标为
，则向量
在基底
下的坐标为（ ）
A ． B ．
C ． D ．
难度：
知识点：平面向量
使用次数：158
【答案】
B
【分析】根据空间向量的基本定理和坐标表示即得结果 .
【详解】设 在基底
下的坐标为
，
则 ，
所以 ，
解得 ，
故 在基底
下的坐标为
.
故选： B.
4.
已知向量 是空间的一个基底，向量
是空间的另一个基底，一向量
在基底
下的坐标为
，则向量
在基底
下的坐标为（ ）
A ． B ．
C ． D ．
难度：
知识点：空间中的向量与立体几何
使用次数：185
【答案】
B
【分析】设向量 在基底
下的坐标为
，根据向量列出方程，得出关于
的方程组，求得
的值，即可求解 .
【详解】设向量 在基底
下的坐标为
，
则 ，
所以 ，解得
，
所以向量 在基底
下的坐标为
.
故选： B.
5.
如图，在平行六面体 中，以顶点 A 为端点的三条棱长均为 6 ，且它们彼此的夹角都是 60° ，下列说法中不正确的是（ ）
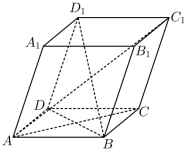
A ．
B ． BD ⊥ 平面 ACC ₁
C ．向量 与
的夹角是 60°
D ．直线 BD ₁ 与 AC 所成角的余弦值为
难度：
知识点：点 直线 平面之间的位置
使用次数：164
【答案】
C
【分析】利用空间向量法，通过计算线段长度、向量夹角、线线角以及证明线面垂直等知识确定正确答案 .
【详解】以 为空间一组基底 .
，
，
所以 ， A 选项正确 .
由于四边形 是菱形，所以
，
，
，
所以 ，即
，
由于 ，所以
平面
， B 选项正确 .
，三角形
是等边三角形，
由图可知 与
的夹角为钝角，也即
与
的夹角为钝角， C 选项错误 .
，
，
所以 .
，
，
所以 .
.
设直线 与直线
所成角为
，
则 ， D 选项正确 .
故选： C
本卷还有30题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
35
总体难度：
中等
难度统计
难度系数
数量
占比
容易
13
37.14%
中等
14
40.0%
偏难
4
11.42%
基础
4
11.42%
题型统计
大题类型
数量
占比
选择题
10
28.57%
填空题
10
28.57%
解答题
10
28.57%
未分类
5
14.28%
知识点统计
知识点
数量
占比
空间中的向量与立体几何
18
51.42%
平面向量
6
17.14%
点 直线 平面之间的位置
10
28.57%
三角函数
1
2.85%
版权提示
该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。