用数学归纳法证明 能被 31 整除时,从 k 到
添加的项数共有( )项
A . 7 B . 6 C . 5 D . 4
C
【分析】分别写出 与
时相应的代数式,对比观察求解 .
【详解】当 时,则
当 时,则
∴ 从 k 到 添加的项数共有 5 项
故选: C.
已知数列 的前
项和为
,
,且对任意的
均有
,则下列三个命题中,所有真命题的序号是( )
① 存在实数 ,使得
为等差数列;
② 存在实数 ,使得
为等比数列;
③ 若存在 ,使得
,则实数
唯一 .
A . ① B . ①③ C . ②③ D . ①②③
A
【分析】 先求出
,由此容易判断 ①② ,对于 ③ ,当
为偶数时,
,当
为奇数时,
, 若存在
,使得
, 则
,且
,由此可分
为奇数和偶数讨论即可判断
【详解】因为 ,
所以 ,则
,
所以数列 、
为等差数列,且公差为 2 ,
由 ,
得
,
所以
,
① 当 时,
,所以
,所以
为等差数列, ① 对;
② 若存在实数 ,使得
为等比数列,则
,即
,
因为方程组无解,所以 不可能为等比数列, ② 错;
③ 当 为偶数时,因为
,
,
,
,
将上述各式相加,可得
,
当 为奇数时,
,
若存在 ,使得
,所以
,且
,
当 为偶数时,
,解得
;
当 为奇数时,
,解得
,
所以 不唯一, ③ 错.
故选: A
数列 满足
,
,则下列说法正确的是( )
A .若 ,则数列
单调递减
B .若存在无数个自然数 ,使得
,则
C .当 时,
的最小值不存在
D .当 时,
恒成立
D
【分析】利用递推关系研究数列的单调性即可逐一作出判断 .
【详解】由 ,得
,
对于 若数列
单调递减,则
,即各项不为 1 , ∴
且
, ∴
且
,故
且
,故 A 错误;
对于 :当
或
时,
,存在无数个自然数
,使得
,故
错误;
对于 :当
时,
,所以
的最小值为 1 ,故
错误;
对于
时,
,
,又由以上推理知
递减,所以
,
设 ,
,
,
,
,
依次类推, ,
所以 ,
综上,对任意 ,
正确.
故选: .
已知数列 满足
,
(
),记
为数列
的前
项和,则( )
A . B .
C .
D .
B
【分析】显然该数列是正项数列,利用 得到一个范围,另外合理变形递推关系,得到数列的通项的范围,然后利用裂项相消法解决 .
【详解】因为 ,所以
,所以
,
,于是
,故
,由累加法可得当
时,
,而当
时,
也成立,所以
,于是
,
故 ,故
,由累乘法可得当
时,
,所以
,所以
.
故选: B
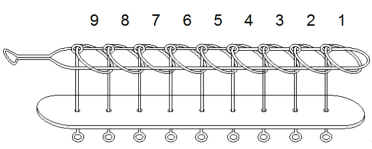
九连环是一种流传于我国民间的传统智力玩具 . 它用九个圆环相连成串,以解开为胜 . 它在中国有近两千年的历史,《红楼梦》中有林黛玉巧解九连环的记载 . 周邦彦也留下关于九连环的名句 “ 纵妙手、能解连环 .” 九连环有多种玩法,在某种玩法中 : 已知解下 1 个圆环最少需要移动圆环 1 次,解下 2 个圆环最少需要移动圆环 2 次,记 为解下
个圆环需要移动圆环的最少次数,且
,则解下 8 个圆环所需要移动圆环的最 少次数为( )
A . 30 B . 90 C . 170 D . 341
C
【分析】根据 ,逐个代入
,即可求解 .
【详解】由题, ,所以
.
故选 . : C
本卷还有30题,登录并加入会员即可免费使用哦~

该作品由: 用户郑琴分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。