2005年普通高等学校招生全国统一考试数学试卷（全国卷.文）
高中
整体难度：中等
2009-03-16
题号
一
二
三
四
五
评分
一、计算题 (共16题)
添加该题型下试题
1.
已知数列
的首项
前
项和为
，且
（I）证明数列
是等比数列；
（II）令
，求函数
在点
处的导数
。
难度：
知识点：数列
使用次数：191
【答案】
解：（I）由已知
，
∴
两式相减得
即
,
从而
.
当
时
∴
.
又
,∴
从而
.
故总有，n∈N*.
又∵∴
从而
，
即数列
是以为
首项，2为公比的等比数列。
（II）由（I）知
。
∵
∴
从而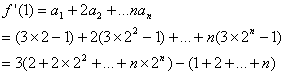
2.
ABC中，内角A、B、C的对边分别是a、b、c，已知a、b、c成等比数列，且
（Ⅰ）求
的值
（Ⅱ）设
，求a+ c的值。
难度：
知识点：三角函数
使用次数：136
【答案】
解：（Ⅰ）由
得
由
及正弦定理得
于是
=
=
=
=
=
=
（Ⅱ）由
得
，由可得
，即
由余弦定理
得
=5
=5+4=9
∴ 
3.
设甲、乙、丙三台机器是否需要照顾相互没有影响，已知在某一小时内，甲、乙都需要照顾的概率为0.05，甲、丙都需要照顾的概率为0.1，乙、丙都需要照顾的概率为0.125
（Ⅰ）求甲、乙、丙每台机器在这个小时内需要照顾的概率分别为多少；
（Ⅱ）计算这个小时内至少有一台机器需要照顾的概率
难度：
知识点：概率
使用次数：132
【答案】
解：记“机器甲需要照顾”为事件A，“机器乙需要照顾”为事件B，“机器丙需要照”为事件C，由题意，各台机器是否需要照顾相互之间没有影响，因此，A、B、C是相互独立事件。
（Ⅰ）由已知得
解得：
，
，
所以甲、乙、丙每台机器需要照顾的概率分别为0.2，0.25，0.5
（Ⅱ）记
的对立事件为
，
的对立事件为
，
的对立事件为
，
则：
，
，
于是
所以这个小时内至少有一台机器需要照顾的概率为0.7
4.
已知二次函数
的二次项系数为
，且不等式
的解集为
。
（Ⅰ）若方程
有两个相等的根，求的解析式；
（Ⅱ）若的最大值为正数，求的取值范围。
难度：
知识点：函数的应用
使用次数：134
【答案】
解：（I）∵f(x)+2x>0的解集为（1，3），
∴f(x)+2x=a(x-1)(x-3),且a<0.因而
f(x)=a(x-1)(x-3)-2x=ax2-(2+4a)x+3a. ①
由方程f(x)+6a=0得
ax2-(2+4a)x+9a=0. ②
因为方程②有两个相等的根，所以△=[-(2+4a)]2-4a・9a=0,
即 5a2-4a-1=0. 解得 a=1或a=-
.
由于a<0，舍去a=1.将a=-代入①得f(x)的解析式 f(x)=-x2-
x-
.
(II)由f(x)=ax2-2(1+2a)x+3a
=a(x-
)2-
及a<0，可得f(x)的最大值为-.
由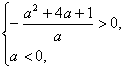
解得 a<-2-
或-2+<a<0.
故当f(x)的最大值为正数时，实数a的取值范围是(-∞，-2-)∪(-2+,0).
5.
已经知{an}是各项为不同的正数的等差数列lga1、lga2、lga4成等差数列.又bn=
,n=1,2,3,……。
（Ⅰ）证明{bn}为等比数列；
（Ⅱ）如果数列{bn}前3项的和等于
，求数列{an}的首项a1和公差d。
难度：
知识点：数列
使用次数：149
【答案】
解 （Ⅰ）证明：∵lga1、lga2、lga4成等差数列，∴2lga2=lga1+lga4，即即a
=a1・a4
又设等差数列{an}的公差为d，则 (a1+d)2=a1(a1+3d),
这样 d2= a1d 从而 d(d- a1)=0
∵d≠0 ∴d=a1≠0
=a1+(2n-1)d=2nd
bn=
=
这时{bn}是首项b1=
，公式为
的等比数列。
（Ⅱ）解：
∵b1+b2+b3=(1++
)=
，∴d=3,
所以a1=d=3
本卷还有22题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
27
总体难度：
中等
难度统计
难度系数
数量
占比
偏难
3
11.11%
容易
8
29.62%
中等
16
59.25%
题型统计
大题类型
数量
占比
计算题
16
59.25%
综合题
2
7.40%
填空题
7
25.92%
选择题
2
7.40%
知识点统计
知识点
数量
占比
数列
4
14.81%
三角函数
4
14.81%
圆锥曲线与方程
4
14.81%
点 直线 平面之间的位置
3
11.11%
概率
5
18.51%
函数的应用
4
14.81%
导数及其应用
1
3.70%
圆与方程
1
3.70%
计数原理
1
3.70%
版权提示
该作品由: 用户454454分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。