广西高中数学高考真题125714
高中
整体难度：中等
2017-04-16
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
已知集合A={x|x2+5x＞0}，B={x|﹣3＜x＜4}，则A∩B等于（ ）
A．（﹣5，0） B．（﹣3，0） C．（0，4） D．（﹣5，4）
难度：
知识点：集合与函数的概念
使用次数：140
【答案】
C【考点】交集及其运算．
【分析】求出关于A的解集，从而求出A与B的交集．
【解答】解：∵A={x||x2+5x＞0}={x|x＜﹣5或x＞0}，B={x|﹣3＜x＜4}，
∴A∩B={x|0＜x＜4}，
故选：C．
2.
已知复数z满足
=
（a∈R），若z的虚部为﹣3，则z的实部为（ ）
A．﹣1 B．1 C．3 D．5
难度：
知识点：数系的扩充与复数的引入
使用次数：188
【答案】
B【考点】复数代数形式的乘除运算．
【分析】把已知等式变形，利用复数代数形式的乘除运算化简，再由z的虚部为﹣3求得a值，则答案可求．
【解答】解：∵
=
，
∴
=（2+ai）（1﹣i）=2+a+（a﹣2）i，
∴a﹣2=﹣3，即a=﹣1．
∴实部为2+a=2﹣1=1．
故选：B．
3.
某仪器厂从新生产的一批零件中随机抽取40个检测，如图是根据抽样检测后零件的质量（单位：克）绘制的频率分布直方图，样本数据分8组，分别为[80，82），[82，84），[84，86），[86，88），[88，90），[90，92），[92，94），[94，96]，则样本的中位数在（ ）
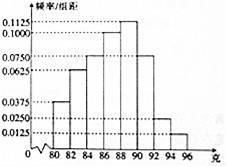
A．第3组 B．第4组 C．第5组 D．第6组
难度：
知识点：统计
使用次数：196
【答案】
B【考点】频率分布直方图．
【分析】根据频率分布直方图求出前4组的频数为22，且第四组的频数8，即可得到答案．
【解答】解：由图可得，前第四组的频率为（0.0375+0.0625+0.075+0.1）×2=0.55，
则其频数为40×0.55=22，且第四组的频数为40×0.1×2=8，
故中位数落在第4组，
故选：B
4.
已知数列{an}满足：
=
，且a2=2，则a4等于（ ）
A．﹣ B．23 C．12 D．11
难度：
知识点：数列
使用次数：170
【答案】
D【考点】等比数列的通项公式．
【分析】数列{an}满足：
=
，可得an+1+1=2（an+1），利用等比数列的通项公式即可得出．
【解答】解：∵数列{an}满足： =，∴an+1+1=2（an+1），即数列{an+1}是等比数列，公比为2．
则a4+1=22（a2+1）=12，解得a4=11．
故选：D．
5.
已知角θ的终边过点（2sin2
﹣1，a），若sinθ=2
sin
cos
，则实数a等于（ ）
A．﹣
B．﹣
C．±
D．±
难度：
知识点：三角恒等变换
使用次数：165
【答案】
B【考点】任意角的三角函数的定义．
【分析】利用二倍角公式化简，再利用正弦函数的定义，建立方程，即可得出结论．
【解答】解：2sin2
﹣1=﹣cos
=﹣
，2
sin
cos
=﹣
，
∵角θ的终边过点（2sin2
﹣1，a），sinθ=2
sin
cos
，
∴
=﹣
，
∴a=﹣
，
故选B．
本卷还有18题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
23
总体难度：
中等
难度统计
难度系数
数量
占比
中等
18
78.26%
容易
5
21.73%
题型统计
大题类型
数量
占比
选择题
12
52.17%
填空题
4
17.39%
解答题
7
30.43%
知识点统计
知识点
数量
占比
集合与函数的概念
1
4.34%
数系的扩充与复数的引入
1
4.34%
统计
1
4.34%
数列
2
8.69%
三角恒等变换
1
4.34%
框图
1
4.34%
平面向量
1
4.34%
不等式
2
8.69%
空间几何体
1
4.34%
基本初等函数I
1
4.34%
圆锥曲线与方程
3
13.04%
函数的应用
1
4.34%
计数原理
1
4.34%
球面上的几何
1
4.34%
解三角形
1
4.34%
概率
1
4.34%
点 直线 平面之间的位置
1
4.34%
导数及其应用
1
4.34%
坐标系与参数方程
1
4.34%
版权提示
该作品由: 用户小韦分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。