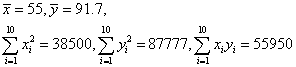2016_2017学年高中数学每日一题（2月27日_3月5日）试卷及答案新人教A版必修3
高中
整体难度：中等
2017-06-21
题号
一
二
三
四
五
评分
一、解答题 (共12题)
添加该题型下试题
1.
下列关系中，属于相关关系的是______．
①人的身高与视力的关系；
②做自由落体运动的物体的质量与落地时间的关系；
③降雪量与交通事故的发生率之间的关系．
（2）有个男孩的年龄与身高的统计数据如下：
| 年龄/岁 | 1 | 2 | 3 | 4 | 5 | 6 |
| 身高/cm | 78 | 87 | 98 | 108 | 115 | 120 |
画出散点图，并判断它们是否有相关关系．如果有相关关系，是正相关还是负相关？
难度：
知识点：统计
使用次数：150
【答案】
（1）①身高与视力无关，不具有函数关系，也不具有相关关系；②自由落体的物体的质量与落地时间无关，不具有相关关系；③降雪量越大，交通事故发生率越高，具有不确定性的相关关系．
（2）散点图是分析变量相关关系的重要工具．作出散点图如下图所示．
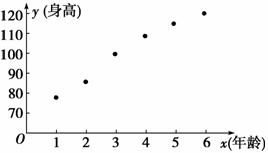
由图可见，男孩年龄与身高具有线性相关关系，且是正相关．
2.
一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，收集数据如下：
| 零件数x（个） | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y（分） | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
（1）y与x是否具有线性相关关系？
（2）如果y与x具有线性相关关系，求y关于x的回归直线方程．
难度：
知识点：统计
使用次数：144
【答案】
（1）画散点图如下：
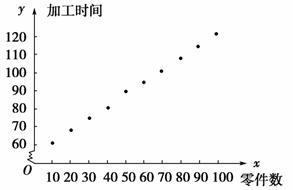
由上图可知y与x具有线性相关关系．
（2）列表、计算：
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| yi | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
| xiyi | 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8640 | 10350 | 12200 |
|
| ||||||||||
，
.
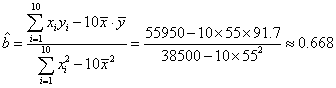即所求的回归直线方程为：
.
3.
设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线如图所示，则以下结论正确的是
A．直线l过点
B．回归直线必通过散点图中的多个点
C．直线l的斜率必在（0,1）内
D．当n为偶数时，分布在l两侧的样本点的个数一定相同
难度：
知识点：直线与方程
使用次数：100
【答案】
A 【解析】A是正确的；回归直线可以不经过散点图中的任何点，故B错误；回归直线的斜率不确定，故C错误；分布在l两侧的样本点的个数不一定相同，故D错误．
4.
某5名学生的总成绩和数学成绩(单位：分)如下表：
| 学生 | A | B | C | D | E |
| 总成绩（ | 482 | 383 | 421 | 364 | 362 |
| 数学成绩（ | 78 | 65 | 71 | 64 | 61 |
（1）画出散点图；
（2）求数学成绩对总成绩的回归方程.
难度：
知识点：统计
使用次数：131
【答案】
【解析】（1）散点图
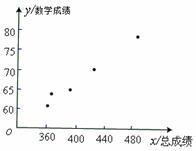
（2）依据题意，得
=402.4, 
=67.8,
=819794, 
=137760，
而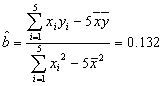
，
，
所以
.
5.
下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量
（吨）与相应的生产能耗
（吨标准煤）的几组对照数据：
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出回归方程
；
（3）已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据（2）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？
难度：
知识点：统计
使用次数：137
【答案】
（1）散点图，如图所示：
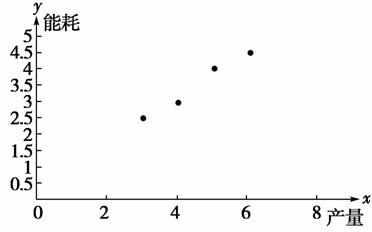
（2）由题意，得
，
，
，
，
∴
，
，
故线性回归方程为
．
（3）根据回归方程的预测，现在生产100吨产品消耗的标准煤为
（吨），
故耗能减少了
（吨）标准煤．
本卷还有29题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
34
总体难度：
中等
难度统计
难度系数
数量
占比
中等
21
61.76%
容易
13
38.23%
题型统计
大题类型
数量
占比
解答题
12
35.29%
选择题
21
61.76%
填空题
1
2.94%
知识点统计
知识点
数量
占比
统计
28
82.35%
直线与方程
1
2.94%
概率
1
2.94%
算法初步
3
8.82%
框图
1
2.94%
版权提示
该作品由: 用户戴东阳分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。