在数列![]() 中,
中,![]() ,
,![]() ,其中
,其中![]() .
.

(1)证明:
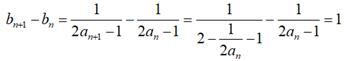
![]() 数列
数列![]() 为等差数列
为等差数列
(2)解:假设数列![]() 中存在三项,它们可以构成等差数列;不妨设为第
中存在三项,它们可以构成等差数列;不妨设为第![]() ,
,![]() ,
,![]() (
(![]() )项,由(1)得
)项,由(1)得![]()
又![]() 为偶数,
为偶数,![]() 为奇数.故不存在这样的三项,满足条件.
为奇数.故不存在这样的三项,满足条件.
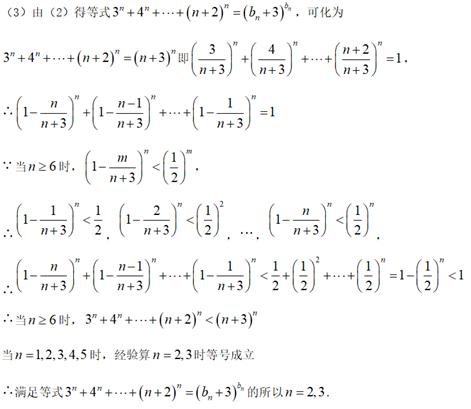
已知函数![]() ,且
,且![]() 的解集为
的解集为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(3)设![]() ,若对于任意的
,若对于任意的![]() 都有
都有![]() ,求
,求![]() 的最小值.
的最小值.
解:(1)∵![]() 的解集为
的解集为![]() ,即
,即![]() 的根为
的根为![]() ,2,
,2,
∴![]() ,
,![]() ,即
,即![]() ,
,![]() ;∴
;∴![]() ;
;

几千年的沧桑沉淀,凝练了黄山的美,清幽秀丽的自然风光,文化底蕴厚重的旅游环境.自明清以来,文人雅士,群贤毕至,旅人游子,纷至沓来,使黄山成为名嗓江南的旅游热点.如图,游客从黄山风景区的景点![]() 处下山至
处下山至![]() 处有两种路径,一种是从
处有两种路径,一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 乘景区观光车到
乘景区观光车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() 米/分钟,在甲出发2分钟后,乙从
米/分钟,在甲出发2分钟后,乙从![]() 乘观光车到
乘观光车到![]() ,在
,在![]() 处停留
处停留![]() 分钟后,再从
分钟后,再从![]() 匀速步行到
匀速步行到![]() .假设观光车匀速直线运行的速度为
.假设观光车匀速直线运行的速度为![]() 米/分
米/分
钟,山路![]() 长为
长为![]() 米,经测量,
米,经测量,![]() ,
,![]() .
.
(1)求观光车路线![]() 的长;
的长;
(2)乙出发多少分钟后,乙在观光车上与甲的距离最短.

(1)在![]() 中,因为
中,因为![]() ,
,
所以![]() ,
,
从而![]()
![]() =
=![]()
![]()
由正弦定理![]() ,得
,得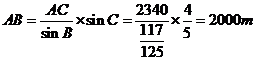 ,
,
所以观光车路线![]() 的长为
的长为![]()
(2)假设乙出发![]() 分钟后,甲、乙两游客距离为
分钟后,甲、乙两游客距离为![]() ,此时甲行走了
,此时甲行走了![]() ,乙距离
,乙距离![]() 处
处![]() ,由余弦定理得
,由余弦定理得
![]()
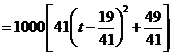
因![]() ,即
,即![]() ,故当
,故当![]() 时,甲,乙两游客的距离最短;
时,甲,乙两游客的距离最短;
在党中央的英明领导下,在全国人民的坚定支持下,中国“抗击新型冠状肺炎”的战役取得了阶段性胜利,现在全国人民积极加入到复工复产的经济建设中.小明在某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪![]() 元,每派送一单奖励
元,每派送一单奖励![]() 元;乙方案:底薪
元;乙方案:底薪![]() 元,每日前
元,每日前![]() 单没有奖励,超过
单没有奖励,超过![]() 单的部分每单奖励
单的部分每单奖励![]() 元.
元.
(1)请分别求出甲、乙两种薪酬方案中日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)根据该公司所有派送员![]() 天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
| 日均派送单数 | 52 | 54 | 56 | 58 | 60 |
| 频数(天) | 20 | 30 | 20 | 20 | 10 |
回答下列问题:
①根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出这100天中甲、乙两种方案的日薪
(单位:元),试分别求出这100天中甲、乙两种方案的日薪![]() 平均数及方差;
平均数及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:![]() ,
,![]() )
)
(1)甲:![]()
乙: 
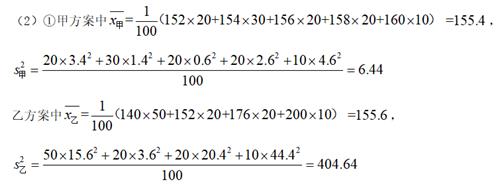
②、答案一:
由以上的计算可知,虽然![]() ,但两者相差不大,且
,但两者相差不大,且![]() 远小于
远小于![]() ,即甲方案日薪收入波动相对较小,所以小明应选择甲方案.
,即甲方案日薪收入波动相对较小,所以小明应选择甲方案.
答案二:
由以上的计算结果可以看出,![]() ,即甲方案日薪平均数小于乙方案日薪平均数,所以小明应选择乙方案.
,即甲方案日薪平均数小于乙方案日薪平均数,所以小明应选择乙方案.
已知向量![]() ,
,![]() ,定义函数
,定义函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)在![]() 中,角
中,角![]() 为锐角,且
为锐角,且![]() ,
,![]() ,求边
,求边![]() 的长.
的长.
(1)![]() ,
,
当![]() 时,
时,![]() 的值域为
的值域为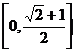
(2)由![]() 得
得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,![]()
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户车车哥分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。