2020山东高一上学期人教A版(2019)高中数学期中考试138238
高中
整体难度：中等
2020-12-29
题号
一
二
三
四
五
评分
一、选择题 (共25题)
添加该题型下试题
1.
集合
.
，则
（ ）
A．
B．
C．
D．
难度：
知识点：集合与函数的概念
使用次数：194
【答案】
B
【分析】
计算出集合
、
，利用交集的定义可得出集合
.
【详解】
，
由于指数函数
是增函数，当
时，
，则
，
因此，
，故选B.
【点睛】
本题考查集合交集运算，同时也考查了函数的定义域与值域的求解，考查计算能力，属于基础题.
2.
若
，则
的取值范围是（ ）
A．
B．
C．
D．
难度：
知识点：基本初等函数I
使用次数：145
【答案】
C
【解析】
试题分析：由解得
，函数
对称轴是
，故在
上递减，
上递增，在处取得最小值为
，在
处取值为
，故值域为.
考点：一元二次不等式.
3.
下列集合中，表示方程组
的解集的是（ ）
A．
B．
C．
D．
难度：
知识点：集合与函数的概念
使用次数：137
【答案】
C
【分析】
解出方程组，方程组的解构成的集合，即有序数对构成的集合.
【详解】
解方程组，得
即
，
所以方程组的解集.
故选：C
【点睛】
此题考查集合元素的辨析，正确解出方程组，方程组的解是有序数对，其解集是由有序数对构成的集合，容易出现概念混淆，把解集的形式弄错.
4.
已知幂函数
，若
，则实数
的取值范围是（ ）
A．
B．
C．
D．
难度：
知识点：基本初等函数I
使用次数：186
【答案】
B
【分析】
由题得函数
在定义域
单调递增，解不等式组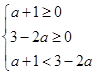
即得解.
【详解】
因为幂函数，所以函数在定义域单调递增，
因为，
所以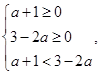
解之得
.
故选：B
【点睛】
本题主要考查幂函数的单调性及其应用，意在考查学生对这些知识的理解掌握水平.
5.
若正数x、y满足
，则
的最小值等于（ ）
A．4 B．5 C．9 D．13
难度：
知识点：基本初等函数I
使用次数：200
【答案】
C
【分析】
由得
（
），代入
后变形，换元后用对勾函数的单调性求解．
【详解】
因为正数x、y满足，所以（），
所以
，令
，
，
，
由对勾函数
在
上单调递减，在
上单调递增，所以
，
所以的最小值为9，此时
．
故选：C．
【点睛】
本题考查用对勾函数的单调性求最值，解题关键是用代入法化二元函数为一元函数，构造对勾函数．变形时一定注意新元取值范围．
本卷还有40题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
45
总体难度：
中等
难度统计
难度系数
数量
占比
容易
16
35.55%
中等
23
51.11%
基础
2
4.44%
偏难
4
8.88%
题型统计
大题类型
数量
占比
选择题
25
55.55%
填空题
8
17.77%
解答题
12
26.66%
知识点统计
知识点
数量
占比
集合与函数的概念
7
15.55%
基本初等函数I
32
71.11%
常用逻辑用语
3
6.66%
不等式
2
4.44%
函数的应用
1
2.22%
版权提示
该作品由: 用户jjl分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。