在二项式![]() 的展开式中,常数项是________;系数为有理数的项的个数是_______.
的展开式中,常数项是________;系数为有理数的项的个数是_______.
![]()
![]()
【分析】
本题主要考查二项式定理、二项展开式的通项公式、二项式系数,属于常规题目.从写出二项展开式的通项入手,根据要求,考察![]() 的幂指数,使问题得解.
的幂指数,使问题得解.
【详解】
![]() 的通项为
的通项为![]()
可得常数项为![]() ,
,
因系数为有理数,![]() ,有
,有![]() 共5个项
共5个项
【点睛】
此类问题解法比较明确,首要的是要准确记忆通项公式,特别是“幂指数”不能记混,其次,计算要细心,确保结果正确.
在![]() 的二项展开式中,
的二项展开式中,![]() 项的系数为 .(结果用数值表示).
项的系数为 .(结果用数值表示).
21.
【解析】
利用二项式展开式的通项公式求得展开式中x2的系数.
【详解】
二项式(1+x)7展开式的通项公式为
Tr+1=![]() •xr,
•xr,
令r=2,得展开式中x2的系数为![]() =21.
=21.
故答案为:21.
【点睛】
求二项展开式有关问题的常见类型及解题策略
(1)求展开式中的特定项.可依据条件写出第r+1项,再由特定项的特点求出r值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第r+1项,由特定项得出r值,最后求出其参数.
![]() 的展开式中x7的系数为__________.(用数字作答)
的展开式中x7的系数为__________.(用数字作答)
![]()
【解析】
试题分析:展开式通项为![]() ,令
,令![]() ,得
,得![]() ,
,
所以展开式中![]() 的系数为
的系数为![]() .故答案为
.故答案为![]() .
.
【考点】二项式定理
【名师点睛】①求特定项系数问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即n,r均为非负整数,且n≥r);第二步是根据所求的指数,再求所要求的项.
②有理项是字母指数为整数的项.解此类问题必须合并通项公式中同一字母的指数,根据具体要求,令其为整数,再根据数的整除性来求解.
4名学生参加3个兴趣小组活动,每人参加一个或两个小组,那么3个兴趣小组都恰有2人参加的不同的分组共有_________种.
90
【分析】
由题意得4名学生中,恰有2名学生参加2个兴趣小组,,其余2 名学生参加一个兴趣小组,然后分情况讨论可得参加的不同的分组的种数.
【详解】
由题意得4名学生中,恰有2名学生参加2个兴趣小组,,其余2 名学生参加一个兴趣小组,首先4名学生中抽出参加2个兴趣小组的学生共有![]() 种.
种.
下面对参加兴趣小组的情况进行讨论:
参加两个兴趣小组的同学参加的兴趣小组完全相同,共![]() 种;
种;
2、参加两个兴趣小组的同学参加的兴趣小组有一个相同,共![]() 种.
种.
故共有![]() 种.
种.
即答案为90.
【点睛】
本题考查两个计数原理,属中档题.
若二项式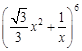 的展开式中的常数项为
的展开式中的常数项为![]() ,则
,则![]() ______.
______.
124
【分析】
先根据二项展开式求得常数项项数,即得常数项,再根据定积分得结果.
【详解】
因为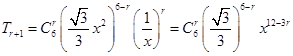 ,
,
所以由![]() 得
得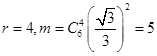 ,
,
因此![]() .
.
【点睛】
求二项展开式有关问题的常见类型及解题策略
(1)求展开式中的特定项.可依据条件写出第![]() 项,再由特定项的特点求出值即可.
项,再由特定项的特点求出值即可.
(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第![]() 项,由特定项得出
项,由特定项得出![]() 值,最后求出其参数.
值,最后求出其参数.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户庄纯洁分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。