高中数学2020年知识点整理——新文化试题分类训练题【含详解】
高中
整体难度：中等
2021-01-06
题号
一
二
三
四
五
评分
一、选择题 (共70题)
添加该题型下试题
1.
据记载，欧拉公式
是由瑞士著名数学家欧拉发现的，该公式被誉为“数学中的天桥”.特别是当
时，得到一个令人着迷的优美恒等式
，这个恒等式将数学中五个重要的数（自然对数的底e，圆周率
，虚数单位
，自然数的单位1和零元0）联系到了一起，有些数学家评价它是“最完美的公式”.根据欧拉公式，若复数z=
的共轭复数为
，则
（ ）
A．
B．
C．
D．
难度：
知识点：数系的扩充与复数的引入
使用次数：152
【答案】
A
【分析】
根据欧拉公式，代入可得复数
，化简后由共轭复数定义即可得
.
【详解】
欧拉公式
，
则
，
根据共轭复数定义可知
，
故选：A.
【点睛】
本题考查了数学文化与简单应用，复数的相关概念和共轭复数定义，属于基础题.
2.
我国古代数学著作《九章算术》中记载问题：“今有垣厚八尺，两鼠对穿，大鼠日一尺，小鼠日半尺，大鼠日增倍，小鼠日自半，问几何日相逢？”，意思是“今有土墙厚8尺，两鼠从墙两侧同时打洞，大鼠第一天打洞一尺，小鼠第一天打洞半尺，大鼠之后每天打洞长度比前一天多一倍，小鼠之后每天打洞长度是前一天的一半，问两鼠几天打通相逢？”两鼠相逢需要的天数最小为（ ）
A．2 B．3 C．4 D．5
难度：
知识点：数列
使用次数：156
【答案】
C
【分析】
设需要n天时间才能打通相逢，则有：
+
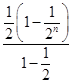≥8，即2n﹣
﹣8≥0，解不等式即可得出.
【详解】
设需要n天时间才能打通相逢，则+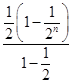≥8，
化为：2n﹣﹣8≥0，令2n=t,则
（舍去）或
∴2n>8, ∴n>3,n的最小整数为4.
故选C．
【点睛】
本题考查了等比数列的求和公式，考查了推理能力与计算能力，属于中档题．
3.
古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆
的中心为原点，焦点
，
均在
轴上，的面积为
，且短轴长为
，则的标准方程为（ ）
A．
B．
C．
D．
难度：
知识点：圆锥曲线与方程
使用次数：193
【答案】
B
【分析】
根据“逼近法”求椭圆的面积公式，及短轴长为
，即可求得
的值，进而由焦点在
轴上可得
的标准方程.
【详解】
由题意可得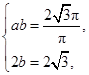
解得
，
，
因为椭圆的焦点在轴上，所以的标准方程为
.
故选：B.
【点睛】
本题考查了数学文化，椭圆的几何性质及标准方程求法，属于基础题.
4.
我国南北朝时期的数学家祖暅提出了计算几何体体积的祖暅原理：“幂势既同，则积不容异“．意思是两个同高的几何体，如果在等高处的截面积都相等，那么这两个几何体的体积相等．现有某几何体和一个圆锥满足祖暅原理的条件，若该圆锥的侧面展开图是半径为3的圆的三分之一，则该几何体的体积为（ ）
A．
π B．
π C．4
D．
难度：
知识点：空间几何体
使用次数：121
【答案】
A
【分析】
由题意可得该几何体的体积与圆锥相同，结合圆锥侧面展开图的特征可求得圆锥的母线与底面半径的长度，进而可得圆锥的高，代入圆锥体积公式即可得解．
【详解】
由题意可知，该几何体的体积等于圆锥的体积，
∵圆锥的侧面展开图恰为一个半径为3的圆的三分之一，
∴圆锥的底面周长为
，
∴圆锥的底面半径为1，母线长为3，
∴圆锥的高为
，
∴圆锥的体积
圆锥
．
从而所求几何体的体积为
．
故选：A．
【点睛】
本题考查了数学文化与圆锥体积的求法，考查了圆锥侧面展开图的特征，正确理解题意是解题的关键，属于基础题．
5.
九连环是我国从古至今广泛流传的一种益智游戏，它用九个圆环相连成串，以解开为胜．据明代杨慎《丹铅总录》记载：“两环互相贯为一，得其关捩，解之为二，又合面为一“．在某种玩法中，用an表示解下n（n≤9，n∈N*）个圆环所需的移动最少次数，若a1＝1．且an＝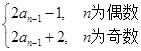
，则解下5个环所需的最少移动次数为（ ）
A．7 B．13 C．16 D．22
难度：
知识点：数列
使用次数：172
【答案】
C
【分析】
根据已知的递推关系求
，从而得到正确答案.
【详解】
，
，
，
，
,
所以解下5个环所需的最少移动次数为16.
故选：C
【点睛】
本题考查以数学文化为背景，考查递推公式求指定项，属于基础题型.
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
容易
52
52.0%
中等
33
33.0%
基础
8
8.0%
偏难
6
6.0%
很难
1
1.0%
题型统计
大题类型
数量
占比
选择题
70
70.0%
填空题
25
25.0%
解答题
5
5.0%
知识点统计
知识点
数量
占比
数系的扩充与复数的引入
2
2.0%
数列
25
25.0%
圆锥曲线与方程
1
1.0%
空间几何体
17
17.0%
框图
5
5.0%
三角函数
8
8.0%
平面向量
2
2.0%
常用逻辑用语
1
1.0%
计数原理
5
5.0%
不等式
8
8.0%
基本初等函数I
8
8.0%
圆与方程
2
2.0%
集合与函数的概念
2
2.0%
概率
3
3.0%
直线与方程
2
2.0%
三角恒等变换
1
1.0%
统计案例
2
2.0%
导数及其应用
3
3.0%
推理与证明
2
2.0%
数学竞赛
1
1.0%
版权提示
该作品由: 用户姜树松分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。