2020河北高三下学期人教B版(2019)高中数学高考模拟138415
高中
整体难度：中等
2021-01-18
题号
一
二
三
四
五
评分
一、解答题 (共12题)
添加该题型下试题
1.
已知函数
.
（1）求曲线
在点
处的切线方程；
（2）证明：
.
难度：
知识点：导数及其应用
使用次数：142
【答案】
（1）
；（2）证明见解析.
【分析】
（1）根据导数的几何意义求出斜率，即可写出切线的方程；
（2）由原不等式可转化为
，构造函数
，
，利用导数分别求最大值与最小值即可求解.
【详解】
（1）由
，得
，
所以切线的斜率
，
又因为当
时，
，
所以切线方程为
，
即.
（2）欲证
，即证
，
即证，
设，则
，，
当
时，
，
在
上单调递增，
当
时，
，在
上单调递减，
所以在处取得极大值，即为最大值，
所以
，
所以
.
设，则
，
所以
在
上单调递增，
所以
，
所以
在
时成立，
所以
，
所以，
所以，
即成立.
【点睛】
本题主要考查了导数的几何意义，切线方程，利用导数求函数的最值，不等式的证明，属于中档题.
2.
如图所示椭圆
的左、右顶点分别为
，
，上、下顶点分别为
，
，右焦点为
，
，离心率
.
（1）求椭圆
的方程；
（2）过点
作斜率为
的直线
与椭圆交于点
，
（点在第一象限），直线
与直线
交于点
，求点的坐标.
难度：
知识点：圆锥曲线与方程
使用次数：195
【答案】
（1）
；（2）
.
【分析】
（1）根据
及
可求
的值，从而可得椭圆的方程.
（2）联立直线方程和椭圆方程可求
的坐标，再求得直线
的方程后可得点
的坐标.
【详解】
解：（1）由及，
可知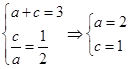
，
所以
，
所以椭圆
的方程为.
（2）依题可设过点
且斜率为
的直线
，
，
，
联立方程组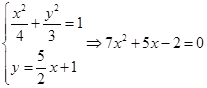
，
解得
，
，则
，
，
所以
，
，
由（1）知，
，
.
所以直线
，①
直线
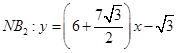，②
由①②，解得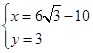
，
所以点的坐标为.
【点睛】
本题考查椭圆方程的求法、直线与椭圆的相交时交点坐标的求法、直线与直线的交点的求法，后两者均需联立曲线的方程，消元后求解即可，本题属于中档题.
3.
如图所示的斜三棱柱
中，点在底面
的投影
为
边的中点，
，
，
，
.
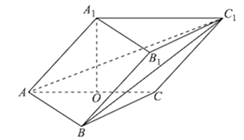
（1）证明：平面
平面
；
（2）求点到平面
的距离.
难度：
知识点：点 直线 平面之间的位置
使用次数：141
【答案】
（1）证明见解析；（2）2.
【分析】
（1）根据
，
，
得到
，再由
为
在底面
，得到
，利用线面垂直的判定定理证得
平面
，进而再利用面面垂直的判定定理证明.
（2）由
平面，得到点
到平面的距离等于点到平面的距离，然后利用等体积法
求解.
【详解】
（1）因为，，，
所以
，
所以
，即.
因为为在底面的投影，
所以
平面，所以.
因为
，所以平面，
又
平面
，
所以平面
平面.
（2）由条件可知，
，
，
所以
，
所以点到平面的距离为.
因为平面，
所以点
到平面的距离等于点到平面的距离，即为
，
且
.
又由，，
，可知
，
所以
，
所以在
中，
，
所以
.
由（1）的证明，可知
平面，
所以
，
所以
.
设点到平面的距离为
，
由等体积法，可知
，
即
，
所以点到平面的距离为2.
【点睛】
本题主要考查线面垂直，面面垂直的判定定理和等体积法求点到面的距离，还考查了转化化归的思想和逻辑推理的能力，属于中档题.
4.
已知
的内角
、
、所对的边为
、
、
，且满足
.
（1）求角的大小；
（2）若的外接圆半径为1，求
的最大值.
难度：
知识点：三角函数
使用次数：239
【答案】
（1）
；（2）.
【分析】
（1）本题首先可根据正弦定理得出
，然后根据二倍角公式得出
，最后根据同角三角函数关系得出
，即可得出结果；
（2）本题首先可根据
的外接圆半径为1得出
，然后根据余弦定理以及基本不等式得出
，即可得出结果.
【详解】
（1）因为
，所以，
因为
，所以
，
，
即，
因为
，所以
，
则
，，
，.
（2）因为的外接圆半径为1，所以
，
则
，
即，当且仅当
时取等号，
故
，
的最大值为.
【点睛】
本题考查解三角形相关问题的求解，考查正弦定理边角互换以及余弦定理的应用，考查通过基本不等式求最值，考查计算能力，考查转化与化归思想，是中档题.
5.
在我国抗击新型冠状病毒肺炎期间，素有“南抖音，北快手”之说的小视频除了给人们带来生活中的快乐外，更在于传递了一种正能量，为抗疫起到了积极的作用，但一个优秀的小视频在有很好的素材与拍摄成品外，更要有制作上的技术要求.某同学为提高自己的制作水平，将所制作的某小视频发到自己的朋友圈里，并请朋友圈的朋友按自己的审美给予评价，通过收集100位朋友（男、女各前50位）的评价，得到下面的列联表：
| 优秀 | 不优秀 | |
| 男性朋友 | 35 | 15 |
| 女性朋友 | 27 | 23 |
（1）分别估计男、女性朋友对该小视频评价优秀的概率；
（2）能否有95%的把握认为对该小视频的制作评价是否优秀与性别有关？
附：
.
|
| 0.050 | 0.010 | 0.001 |
|
| 3.841 | 6.635 | 10.828 |
难度：
知识点：统计案例
使用次数：213
【答案】
（1）0.7；0.54；（2）没有95%的把握认为对该小视频的制作评价是否优秀与性别有关.
【分析】
（1）根据表中数据即可估计出概率；
（2）根据个数计算出卡方值，和3.841比较即可判断.
【详解】
（1）由表中数据，男性朋友对该小视频评价优秀的比率为
，
因此男性朋友对该小视频评价优秀的概率的估计值为0.7.
女性朋友对该小视频评价优秀的比率为
，
因此女性朋友对该小视频评价优秀的概率的估计值为0.54.
（2）由列联表可知，
，
所以没有95%的把握认为对该小视频的制作评价是否优秀与性别有关.
【点睛】
本题考查由频率估计概率，考查独立性检验，属于基础题.
本卷还有38题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
43
总体难度：
中等
难度统计
难度系数
数量
占比
中等
24
55.81%
容易
12
27.90%
偏难
3
6.97%
基础
4
9.30%
题型统计
大题类型
数量
占比
解答题
12
27.90%
填空题
8
18.60%
选择题
23
53.48%
知识点统计
知识点
数量
占比
导数及其应用
3
6.97%
圆锥曲线与方程
5
11.62%
点 直线 平面之间的位置
2
4.65%
三角函数
5
11.62%
统计案例
4
9.30%
不等式选讲
1
2.32%
坐标系与参数方程
1
2.32%
空间几何体
2
4.65%
圆与方程
2
4.65%
数列
3
6.97%
不等式
2
4.65%
框图
2
4.65%
平面向量
2
4.65%
函数的应用
1
2.32%
集合与函数的概念
2
4.65%
数系的扩充与复数的引入
2
4.65%
基本初等函数I
3
6.97%
计数原理
1
2.32%
版权提示
该作品由: 用户崔子贤分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。