已知![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() 是两个不同的平面,给出下列命题:
是两个不同的平面,给出下列命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③若
;③若![]() ,
,![]() 是异面直线,则存在
是异面直线,则存在![]() ,
,![]() ,使
,使![]() ,
,![]() ,且
,且![]() ;④若
;④若![]() ,
,![]() 不垂直,则不存在
不垂直,则不存在![]() ,使
,使![]() .
.
其中正确的命题有( ).
A.1个 B.2个 C.3个 D.4个
B
【分析】
①,②,③借助长方体可直接判断对错,④通过反证法假设结论存在,通过面面垂直的判定得出与已知矛盾,即可判断出④正确.
【详解】
①由图可知符合:![]() ,
,![]() ,
,![]() ,
,

但![]() ,
,![]() 为异面直线,不平行,故①错误.
为异面直线,不平行,故①错误.
②由图知符合:![]() ,
,![]() ,
,

但![]() ,故②错误.
,故②错误.
③根据条件:![]() ,
,![]() 是异面直线,则存在
是异面直线,则存在![]() ,
,![]() ,使
,使![]() ,
,![]() ,可画出
,可画出![]() ,
,
如图所示: ,即存在
,即存在![]() ,故③正确.
,故③正确.
④假设:![]() ,
, ![]() ,由平面与平面垂直的判定可得:
,由平面与平面垂直的判定可得:![]() ,与已知矛盾,
,与已知矛盾,
故![]() ,
,![]() 不垂直,则不存在
不垂直,则不存在![]() ,使
,使![]() ,④正确.
,④正确.
故选:B
【点睛】
本题考察了空间中直线与直线,直线与平面,平面与平面的位置关系,主要考查学生的空间想象能力以及空间中位置关系的判断方法,属于中档题.
已知双曲线![]() 的两条渐近线分别与抛物线
的两条渐近线分别与抛物线![]() 交于第一、四象限的A,B两点,设抛物线焦点为F,若
交于第一、四象限的A,B两点,设抛物线焦点为F,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【分析】
求得双曲线的渐近线方程,联立抛物线方程,求得A,B的坐标,以及F的坐标,设AF的倾斜角为![]() ,由二倍角的余弦公式和同角的基本关系式,以及直线的斜率公式,双曲线的离心率公式,计算可得所求值.
,由二倍角的余弦公式和同角的基本关系式,以及直线的斜率公式,双曲线的离心率公式,计算可得所求值.
【详解】
解:双曲线![]() 的两条渐近线方程为
的两条渐近线方程为![]() ,
,
由抛物线![]() 和
和![]() ,联立可得
,联立可得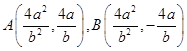 ,
,
由抛物线的方程可得![]() ,
,
设AF的倾斜角为![]() ,斜率为
,斜率为 ,
,
而![]() ,
,
解得![]() (负的舍去),
(负的舍去),
设![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
则![]() ,
,
故选:B.
【点睛】
本题考查双曲线的方程和性质,考查三角函数的恒等变换,以及化简运算能力,属于中档题.
如图,等边![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( )
A.动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
B.恒有平面![]() ⊥平面
⊥平面![]()
C.三棱锥![]() 的体积有最大值
的体积有最大值
D.异面直线![]() 与
与![]() 不可能垂直
不可能垂直
D
【详解】
由题意知,![]() 平面
平面![]() ,固选项A、B正确,
,固选项A、B正确,
对于三棱锥![]() 体积,其底面
体积,其底面![]() 在旋转过程中面积不变,则当
在旋转过程中面积不变,则当![]() 底面
底面![]() 时,三棱锥
时,三棱锥![]() 体积最大,固选项C正确,
体积最大,固选项C正确,
故选D.
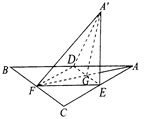
正四面体ABCD的体积为1,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体的公共部分的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【分析】
由题分析,![]() 是正四面体的外接球球心,可得
是正四面体的外接球球心,可得![]() 为
为![]() 的底面的高,即
的底面的高,即![]() 到底面的距离为高的
到底面的距离为高的![]() ,因为两个正四面体关于
,因为两个正四面体关于![]() 对称,则两个对称水平面之间的距离为底面高的
对称,则两个对称水平面之间的距离为底面高的![]() ,即顶点到水平面的距离为底面高的
,即顶点到水平面的距离为底面高的![]() ,进而得到小正四面体的体积为正四面体的
,进而得到小正四面体的体积为正四面体的![]() ,对应四个顶点由四个小正四面体,进而求得公共部分的体积
,对应四个顶点由四个小正四面体,进而求得公共部分的体积
【详解】
若将正四面体![]() 放在一个水平面上,易知其中心到点
放在一个水平面上,易知其中心到点![]() 的距离是
的距离是![]() 到底面距离的
到底面距离的![]() ,所以反射的对称面是距离为
,所以反射的对称面是距离为![]() 到
到![]() 的底面距离
的底面距离![]() 的水平,因此,它割
的水平,因此,它割![]() 点所在的小正四面体时原正四面体的
点所在的小正四面体时原正四面体的![]() ,同理,对
,同理,对![]() 三点处所切割的正四面体也是原正四面体的
三点处所切割的正四面体也是原正四面体的![]() ,则可得到两个正四面体的公共部分体积为
,则可得到两个正四面体的公共部分体积为![]() ,
,
故选:B
【点睛】
本题考查外接球的应用,考查空间想象能力,考查运算能力
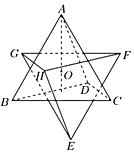
如图,过抛物线![]() 的焦点F的直线依次交抛物线及准线于点A,B,C,若
的焦点F的直线依次交抛物线及准线于点A,B,C,若![]() ,且
,且![]() ,则抛物线的方程为( )
,则抛物线的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
D
【分析】
分别过点![]() 作准线的垂线,分别交准线于点
作准线的垂线,分别交准线于点![]() ,设
,设![]() ,根据抛物线定义可知
,根据抛物线定义可知![]() ,进而推断出
,进而推断出![]() 的值,在直角三角形中求得
的值,在直角三角形中求得![]() ,进而根据
,进而根据![]() ,利用比例线段的性质可求得
,利用比例线段的性质可求得![]() ,则抛物线方程可得.
,则抛物线方程可得.
【详解】
解:如图分别过点![]() 作准线的垂线,分别交准线于点
作准线的垂线,分别交准线于点![]() ,
,
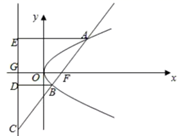
设![]() ,则由已知得:
,则由已知得:![]() ,
,
由定义得:![]() ,故
,故![]() ,
,
在直角三角形![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,从而得
,从而得![]() ,
,
![]() ,
,
![]() 求得
求得![]() ,
,
因此抛物线方程为![]() ,
,
故选:D.
【点睛】
本题主要考查了抛物线的标准方程,考查了学生对抛物线的定义和基本知识的综合把握.
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户姚妍分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。