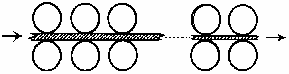
上图为一台冷轧机的示意图;冷轧机由若干对轧辊组成。带钢从一端输人,经过各对轧辊逐步减薄后输出。
(1)输入带钢的厚度为![]() ,输出带钢的厚度为
,输出带钢的厚度为![]() ,若每对轧辊的减薄率不超过
,若每对轧辊的减薄率不超过![]() ,问冷轧机至少需要安装多少对轧辊?
,问冷轧机至少需要安装多少对轧辊?
(一对辊减薄率=输入该对的带钢厚度-从该对输出的带钢厚度)输入该对的带钢厚度
(Ⅱ)已知一台冷轧机共有4对减薄率为20%的轧辊,所有轧辊周长均为1600mm若第k对轧辊有缺陷,每滚动一周在带钢上压出一个疵点,在冷轧机输出的带钢上,疵点的间距为Lk.为了便于检修,
请计算L1、L2、L3并填入下表(轧钢过程中,带钢宽度不变,且不考虑损耗)
| 轧辊序号k | 1 | 2 | 3 | 4 |
| 疵点间距Lk单位:(mm) | 1600 |
答案
(Ⅰ)解:厚度为α的带钢经过减薄率均为r0的n对轧辊后厚度为α(1-r0)
为使输出带钢的厚度不超过β,冷轧机的轧辊数(以对为单位)应满足α(1-r0)≤β,
即(1-r0)≤![]() .
.
由于(1-r0)>0,![]() >0,对上式两端取对数,得
>0,对上式两端取对数,得![]() (1-r0)≤
(1-r0)≤![]() .
.
由于![]() 1-r0)<0,所以n≥
1-r0)<0,所以n≥![]() .
.
因此,至少需要安装不小于![]() 的整数对轧辊.
的整数对轧辊.
(Ⅱ)解法一:第k对轧辊出口处疵点间距离为轧辊周长,在此处出口的两疵点间带钢的
体积为1600・α(1-r)k・宽度(其中r=20%),
而在冷轧机出口处两疵点间带钢的体积为Lk・α(1-r)4・宽度
因宽度相等,且无损耗,由体积相等得
1600・α(1-r)k=Lk・α(1-r)4(r=20%),
即Lk=1600・0.8k-4.
由此得L3=2000(mm),L2=2500(mm),L1=3125(mm).
填表如下
| 轧辊序号k | 1 | 2 | 3 | 4 |
| 疵点间距Lk(mm) | 3125 | 2500 | 2000 | 1600 |
解法二:第3对轧辊出口疵点间距为轧辊周长,在此处出口的两疵点间带钢体积与冷轧机出口处两疵点间带钢体积相等,因宽度不变,有
1600=L3・(1-0.2),
所以L3=![]() =2000(mm)同理L2=
=2000(mm)同理L2=![]() =2500(mm),L1=
=2500(mm),L1=![]() =3125(mm).
=3125(mm).
填表如下
| 轧辊序号k | 1 | 2 | 3 | 4 |
| 疵点间距Lk(mm) | 3125 | 2500 | 2000 | 1600 |
评述:本小题主要考查等比数列、对数计算等基本知识,考查综合运用数学知识和方法解决实际问题的能力.

 ,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2
,简记为数列{an},其中数列的第一项a1也称首项,an是数列的第n项,也叫数列的通项2