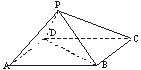
 如图,四棱锥P―ABCD中,底面ABCD为矩形,AB=8,AD=4
如图,四棱锥P―ABCD中,底面ABCD为矩形,AB=8,AD=4![]() ,侧面PAD为等边三角形,并且与底面所成二面角为60°.
,侧面PAD为等边三角形,并且与底面所成二面角为60°.
(Ⅰ)求四棱锥P―ABCD的体积;
(Ⅱ)证明PA⊥BD.
答案
本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析问题的能力.
解:(Ⅰ)如图1,取AD的中点E,连结PE,则PE⊥AD.

图1
作PO⊥平面ABCD,垂足为O,连结OE.
根据三垂线定理的逆定理得OE⊥AD,
所以∠PEO为侧面PAD与底面所成二面角的平面角.
由已知条件可知∠PEO=60°,PE=6,
所以PO=3![]() ,
,
四棱锥P-ABCD的体积
VP-ABCD=![]()
(Ⅱ)解法一:如图1,以O为原点建立空间直角坐标系.通过计算可得
P(0,0,3![]() ),A(2
),A(2![]() ,-3,0),B(2
,-3,0),B(2![]() ,5,0),D(-2
,5,0),D(-2![]() ,-3,0).
,-3,0).
所以![]() =(2
=(2![]() ,-3,-3
,-3,-3![]() ),
), ![]() =(-4
=(-4![]() ,-8,0).
,-8,0).
因为![]() ・
・![]() =-24+24+0=0,
=-24+24+0=0,
所以PA⊥BD.
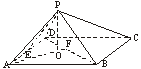
图2
解法二:如图2,连结AO,并延长AO交BD于点F.通过计算可得
EO=3,AE=2![]() ,又由AD=4
,又由AD=4![]() ,AB=8,
,AB=8,
得 ![]() .
.
所以 Rt△AEO∽Rt△BAD,
得 ∠EAO=∠ABD.
所以 ∠EAO+∠ADF=90°,
所以 AF⊥BD.
因为AF为PA在平面ABCD内的射影,
所以 PA⊥BD.


 。
。  α∩β=l,且P∈l。
α∩β=l,且P∈l。