设f（x）=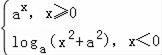
，且f（2）=4，则f（﹣2）等于（ ）
A．1 B．2 C．3 D．4
答案
C【考点】函数的值．
【分析】由已知得f（2）=a2=4，由a是对数的底数，得a=2，由此能求出f（﹣2）．
【解答】解：∵f（x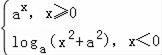）=，且f（2）=4，
∴f（2）=a2=4，解得a=±2，
∵a是对数的底数，∴a≠﹣2，∴a=2，
∴f（﹣2）=log2（4+4）=3．
故选：C．
【点评】本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
设f（x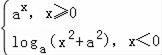）=，且f（2）=4，则f（﹣2）等于（ ）
A．1 B．2 C．3 D．4
C【考点】函数的值．
【分析】由已知得f（2）=a2=4，由a是对数的底数，得a=2，由此能求出f（﹣2）．
【解答】解：∵f（x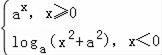）=，且f（2）=4，
∴f（2）=a2=4，解得a=±2，
∵a是对数的底数，∴a≠﹣2，∴a=2，
∴f（﹣2）=log2（4+4）=3．
故选：C．
【点评】本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
分段函数：
1、分段函数：定义域中各段的x与y的对应法则不同，函数式是分两段或几段给出的；
分段函数是一个函数，定义域、值域都是各段的并集。
抽象函数：
我们把没有给出具体解析式的函数称为抽象函数；
一般形式为y=f（x），或许还附有定义域、值域等，如：y=f（x），（x＞0，y＞0）。
知识点拨：
1、绝对值函数去掉绝对符号后就是分段函数。
2、分段函数中的问题一般是求解析式、反函数、值域或最值，讨论奇偶性单调性等。
3、分段函数的处理方法：分段函数分段研究。
登录并加入会员可无限制查看知识点解析
