已知三棱锥
的底面是以
为斜边的等腰直角三角形，且
，则该三棱锥的外接球的体积为( )
A. 
B. 
C. 
D. 
答案
D
【解析】
【分析】
根据三棱锥
的底面是以为斜边的等腰直角三角形，
，可得S在面ABC上的射影为AB中点H，
平面
，在面SHC内作SC的垂直平分线MO与SH交于O，则O为SABC的外接球球心，OS为球半径，由此可得该三棱锥的外接球的体积.
【详解】因为三棱锥的底面是以
为斜边的等腰直角三角形，，
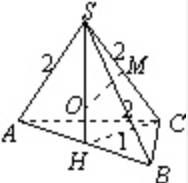
所以S在ABC上的射影为AB中点H，所以平面，
所以SH上任意一点到A,B,C的距离相等，
因为
，在面SHC内作SC的垂直平分线MO与SH交于O，
则O为的外接球球心，
所以
，
即
，解得
，
所以该三棱锥的外接球的体积为
，故选D.
【点睛】该题考查的是有关球的体积的问题，涉及到的知识点是三棱锥的外接球，在解题的过程中，需要明确几何体的外接球的特征，注意思考球心所处的位置，建立相应的等量关系，求得半径，利用公式求得体积.
；
倍. 
.
. 
B
C