如图，三棱台DEF—ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，DC =2BC．

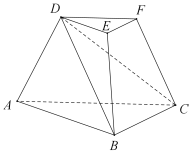
（I）证明：EF⊥DB；

（II）求DF与面DBC所成角的正弦值．

答案

（I）证明见解析；（II）

【解析】

【分析】

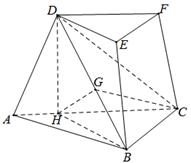
（I）作交于，连接，由题意可知平面，即有，根据勾股定理可证得，又，可得，，即得平面，即证得；

（II）由，所以与平面所成角即为与平面所成角，作于，连接，即可知即为所求角，再解三角形即可求出与平面所成角的正弦值．

详解】（I）作交于，连接．

∵平面平面，而平面平面，

∴平面，即有．

∵，

∴．

在中，，即有，∴．

由棱台的定义可知，，所以，，而，

∴平面，而平面，∴．

（II）因为，所以与平面所成角即为与平面所成角．

作于，连接，由（1）可知，平面，所以平面平面，而平面平面，∴平面．

即在平面内的射影为，即为所求角．

在中，设，则，，

∴．

故与平面所成角的正弦值为．

【点睛】本题主要考查空间点、线、面位置关系，线面垂直的判定定理的应用，直线与平面所成的角的求法，意在考查学生的直观想象能力和数学运算能力，属于基础题．