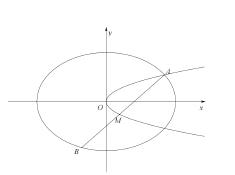
如图，已知椭圆
，抛物线
，点A是椭圆
与抛物线
的交点，过点A的直线l交椭圆于点B，交抛物线于M（B，M不同于A）．
（Ⅰ）若
，求抛物线的焦点坐标；
（Ⅱ）若存在不过原点的直线l使M为线段AB的中点，求p的最大值．
答案
（Ⅰ）
；（Ⅱ）
【解析】
【分析】
（Ⅰ）将p代入方程求得抛物线方程即可得到焦点坐标；
（Ⅱ）设
，联立直线与椭圆方程得到根与系数的关系，进一步得到M的坐标，进一步得到关于
的方程，联立直线与抛物线方程得到
，再联立抛物线与椭圆方程得到
，即可建立方程，再利用基本不等式求最值即可.
【详解】（Ⅰ）当时，的方程为
，故抛物线的焦点坐标为；
（Ⅱ）设
由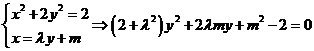
由M在抛物线上，所以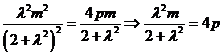
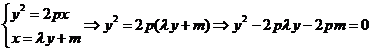
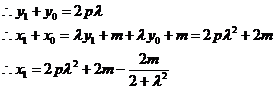
由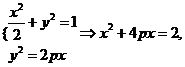
即
所以
，
，
，
所以，
的最大值为，此时
.
【点晴】本题主要考查直线与圆锥曲线的位置关系的综合应用，涉及到求函数的最值，考查学生的数学运算能力，是一道有一定难度的题.
