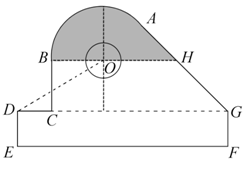
某中学开展劳动实习，学生加工制作零件，零件的截面如图所示．O为圆孔及轮廓圆弧AB所在圆的圆心，A是圆弧AB与直线AG的切点，B是圆弧AB与直线BC的切点，四边形DEFG为矩形，BC⊥DG，垂足为C，tan∠ODC=，，EF=12 cm，DE=2 cm，A到直线DE和EF的距离均为7 cm，圆孔半径为1 cm，则图中阴影部分的面积为________cm²．

答案

【解析】

【分析】

利用求出圆弧所在圆的半径，结合扇形的面积公式求出扇形的面积，求出直角的面积，阴影部分的面积可通过两者的面积之和减去半个单位圆的面积求得.

【详解】设，由题意，，所以，

因为,所以，

因为，所以，

因为与圆弧相切于点，所以，

即为等腰直角三角形；

在直角中，，，

因为，所以，

解得；

等腰直角的面积为；

扇形的面积，

所以阴影部分的面积为.

故答案为：.

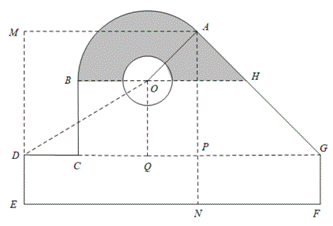
【点睛】本题主要考查三角函数在实际中应用，把阴影部分合理分割是求解的关键，以劳动实习为背景，体现了五育并举的育人方针.