已知直四棱柱ABCD–A1B1C1D1的棱长均为2,∠BAD=60°.以![]() 为球心,
为球心,![]() 为半径的球面与侧面BCC1B1的交线长为________.
为半径的球面与侧面BCC1B1的交线长为________.
答案
![]() .
.
【解析】
【分析】
根据已知条件易得![]()
![]() ,
,![]() 侧面
侧面![]() ,可得侧面
,可得侧面![]() 与球面的交线上的点到
与球面的交线上的点到![]() 的距离为
的距离为![]() ,可得侧面
,可得侧面![]() 与球面的交线是扇形
与球面的交线是扇形![]() 的弧
的弧![]() ,再根据弧长公式可求得结果.
,再根据弧长公式可求得结果.
【详解】如图:
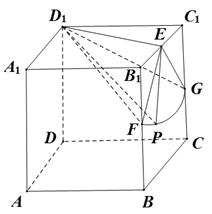
取![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,
,
因为![]() 60°,直四棱柱
60°,直四棱柱![]() 的棱长均为2,所以△
的棱长均为2,所以△![]() 为等边三角形,所以
为等边三角形,所以![]()
![]() ,
,![]() ,
,
又四棱柱![]() 为直四棱柱,所以
为直四棱柱,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 侧面
侧面![]() ,
,
设![]() 为侧面
为侧面![]() 与球面的交线上的点,则
与球面的交线上的点,则![]() ,
,
因为球的半径为![]() ,
,![]() ,所以
,所以![]() ,
,
所以侧面![]() 与球面的交线上的点到
与球面的交线上的点到![]() 的距离为
的距离为![]() ,
,
因为![]() ,所以侧面
,所以侧面![]() 与球面的交线是扇形
与球面的交线是扇形![]() 的弧
的弧![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以根据弧长公式可得![]() .
.
故答案为:![]() .
.
【点睛】本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,属于中档题.
